Discrete Dynamic Lab, update Nov 2005


	part of a basin of attraction of a value v=4, neighborhood k=3, size n=9, 1d cellular automaton, with the nodes shown in 2d. Below: the color scheme for v=4 cell values.




	complex kcode with many emerging gliders, glider guns, and self-replicating structures, on hex lattice. Click to enlarge, click here for info.



	1d n=150 v=8 k=5 k-totalistic Altenberg rule, where lookup table entries are set according to a probability which depends on the frequency of colors in each neighborhood. This example was filtered to emphasise gliders. Click to enlarge.

Discrete Dynamics Lab

Update Nov 2005

(revised from previous updates Dec 04 and Sept 04)

DDLab Version m05: multi value logic, totalistic rules, many new features

Univ of Sussex
www.ddlab.com, Santa Fe, New Mexico

return to: DDLab home - DD-Life - Multi-Value examples

The most significant changes since the last binary release:

Generalizing all aspects of DDLab for multi-value logic (up to 8 values or colors), instead of just Boolean logic (0,1). Click here for some examples.
Constraining DDLab to run forward only for two types of totalistic rules, which allows larger neighborhoods (up to k=25). In 2d the neighborhoods are predefined to make both square or hexagonal lattices. Many interesting "life"-like and other complex dynamics can be found in this constrained rule-space in 2d and 3d. Click here for examples, details and instructions for running these complex rules.
Version m05 extends t- and k-totalistic rules to allow outer-totalistic rules of each type (just for cellular automata). Outer-totalistic rules (also called semi-totalistic rules) allow a different rule depending on the central cell's value (color), so consist of v sub-rules. The game-of-Life is a v=2 outer-totalistic rule.
Reaction-Diffusion dynamics (excitable media), scrolling 2d space-time patterns, and other new features, improvements, revisions and bug fixes.

Multi-value DDLab includes many other new features, improvements and revisions, both major and minor, since the last official release in May 2002. Some of these, but not all, are listed below. The usual harvest of bugs have also been fixed (and not too may added - we hope!).

Code: written in c, is available on request subject to some conditions.
Software: the compiled software for Mac, Linux, Cygwin, Unix, Irix and Dos can be downloaded from the DDLab home page.
Manual: The DDLab manual released in July 2001 (that corresponds to DDLab Version 24) needs to be updated - we're working on it. Most explanations in it can be reinterpreted for the multi-value version by the astute reader. In the meantime this web page can serve as a temporary reference for some of the changes.

For previous updates since March 96,
click Dec 03, July 01, Feb 99, Sept 97.

Some new features and changes

Forward only for just totalistic rules
Multi-value logic
Totalistic and outer-totalistic rules
2d neighborhoods (square and hex) updated
Toggling between square and hex presentation
Setting rules/states updated
Classification of rule-space and complex rule samples
New/revised on-the-fly options
Falling of edge boundary conditions
Scrolling 2d space-time patterns
Reaction-Diffusion Dynamics, Excitable Media

Forward only for just totalistic rules


	complex kcode with emerging spirals on hex lattice. click to enlarge, click here for info

This constrains DDLab:
- to run forward only, to generate and analyze space-time patterns, and disable all basin of attraction functions.
- to allow just t-totalistic (tcode) and k-totalistic rules (kcode).
  and outer versions of both rules The "life"-like rules belong to "kcode". (click here for an examples, explanations, instructions).
- to allow outer versions of both tcode and kcode, where v rules are assigned, one for each color of the central cell.

These constraints conserve memory by reducing the size of lookup tables, which allow bigger value-range/neighborhood (v/k) combinations. The max v/k supported is shown on the right.

    v    k   k-totalistic table size
    2   25      26
    3   25     351
    4   25    3276
    5   25   23751
    6   17   26334
    7   13   27132
    8   11   31824

The first prompt in DDLab's main sequence is now...
- Exit-q, graphics setup, randseed, totalistic/forward only-t
- forward only/single basin/subtree-s (def-field):
Enter t to select forward only for just totalistic rules, the prompt changes to...
- Exit-q, graphics setup, randseed, allow basins-b
- totalistic rules and forward only (def):
Enter return to continue, or b to change back.

Multi-value logic

The multi-value version of DDLab allows network elements to have a value range v anywhere from 2 to 8 (see preview). All DDLab functions (those described in the manual plus some new functions) work for multi-value, including setting rules and initial states, attractor basins including compression, in-degree histograms, learning/forgetting, space-time patterns, filtering, input-entropy, automatic classification, samples of glider rules, the reverse algorithms for CA, RBN and random maps, the Z and lambda parameters, the meta-graph, canalizing, the Derrida plot, damage spread, etc. For 2 values, DDLab works much as before, but with various additional functions as will be described.
The second prompt in DDLab's main sequence is now...
Enter the value range (or return for the default, which changes following previous selections).
There is a color scheme for cell values, displayed top right or left at various times.

The neighborhood matrix is generalized for multi-value (and can be rescaled).

v4k3 neighborhood matrix, sets out all possible neighborhoods (vertically) in descending order of their
4-ary decimal equivalents. The rule-table itself assigns a output value for each neighborhood.

Rule tables can become very long with bigger value-range/neighborhood (v/k).

The max v/k supported for full lookup tables (which allow basins of attraction) is shown on the right.

    v    k   k-totalistic table size
    2   13    8162
    3    9   19683
    4    7   16484
    5    6   15629
    6    5    7776
    7    5   16807
    8    4    4096

State-space S also increases rapidly with the value-range v, and network size n (S=vⁿ).

To generate the basin of attraction field (not single basins or subtrees) the max v/n supported is shown on the right.

Totalistic and outer-totalistic rules

The updated prompts for totalistic and outer-totalistic rules are as follows...

If totalistic-only was selected...
- totalistic only: outertot-o/+o, tcode-t, (def-kcode):.
  The outer-totalistic rule options apply if totalistic-only was selected earlier.
  Enter to for outer-totalistic tcode, or o for outer-totalistic kcode. Otherwise.
  enter t for tcode or return for kcode.
otherwise..
- totalistic: tcode-t k-code-k (def-rule):

2d neighborhoods (square and hex) updated

As mentioned earlier, the max neighborhood size when DDLab is constrained to run forward-only, for just totalistic rules, is k=25 (for v>5 k is reduced). For the full lookup table, max-k=13 (for v>3 k is also reduced).

The predefined 2d neighborhoods have been extended up to k=25 on a square and hex lattice. The layouts try to achieve a reasonable symmetry, which is not always possible. Only the symmetric neighbourhoods are shown below, defaults have a black background. If square and hex are equally symmetric, square is the default. The asymmetric layouts not shown can still be selected.
To force hex for any k there is a new option in the top right WIRING prompt.

2d-2 (hex-x) ...enter 2x to force a hex lattice.

Below are the predefined fully or partly symmetric neighborhoods. (defaults with a black background).
Note that the center cell may form part of its neighborhood, or not. If it does it is shown in red.

k=4 k=5 k=6 k=7 k=8 k=9 k=10 k=11 k=12 k=13 k=14 k=15
square
lattice
hex
lattice

k=16 k=17 k=18 k=19 k=20 k=21 k=22 k=23 k=24 k=25
square
lattice
hex
lattice

Toggling between square and hex presentation

In the 2d wiring graphic prompts, there is a new prompt,

CA wiring and tog hex-x

This toggles the lattice presentation between hex and square, changes the highlighted cell's neighborhood to a local CA predefined neighborhood, and toggles the neighborhood between hex and square (if possible).

In the "on the fly" prompts when running forward in 2d, there is a new prompt to change between square or hex presentation,

tog hex (on) ...present status is indicated by (on)/(of)

For CA with a square neighborhood, the 2d space-time pattern will start on a square lattice, if hex on a hex lattice.

Setting rules/states updated

The methods for setting rules and initial states (which are very similar) have been updated for multi-value, and some new methods added. For example...

Creating an initial state with the bit drawing options
for a 2d network, v=8.
- fill-f gives a further prompt for the value (color) to be filled.
- bits-b drawing bits with the mouse or keyboard, the value (color) can be selected.
- printxterm-x to show the lookup table in the xterm window, after setting the rule, backtrack to the rule selection prompt, then enter x.
- in the bits-b drawing options,
  - width-w a new option , allows the line width to be increased from 1 to many cells for a broader brush stroke.
  - toghex-x the 2d layout can be toggled between square and hexagonal.
  - file-F to save patterns or selected patches, or to load patterns, or patches in a selected position.
This is the updated top right prompt with the various bit drawing options if v=4 for 2d...

keys: set/select/draw value 3-0, vert-v
mouse: move-click, draw selected-keep pressed, move-arrows
width-w, togzero:color/dots-^/., pan2d up/down-U/D exp/cont-e/c
rotate-l/r/u/d, divs-i spin-s comp-m, toghex-x file-F accept-ret

Classification of rule-space and complex rule sample

The automatic classification of rule space has been updated for multi-value. Samples of glider/complex rules are available that can be randomly set on-the-fly when running forward, with g,

g..load glider rule

These files are in dd_extra.tar.gz and include the following,

rule sample automatic classification files:

for 1d, v=2, full lookup table, as before but renamed,
- v2k5ss.sta (k=5)
- v2k6ss.sta (k=6)
- v2k6ss.sta (k=7)
for 1d, multi_value, full lookup table,
- v3k3ss.sta (v=3 k=3)
- v4k2ss.sta (v=4 k=2)
- v4k3ss.sta (v=4 k=3)
- v5k2ss.sta (v=5 k=2)
for 2d, multi-valye kcode,
- v3k4bs.sta (v=3 k=4)
- v3k5bs.sta (v=3 k=5)
- v3k6bs.sta (v=3 k=6)
- v3k7bs.sta (v=3 k=7)
- v4k4bs.sta (v=4 k=4)
- v4k6bs.sta (v=4 k=6)

glider/complex rule sample files for loaded on-the-fly with "g":

for 1d, v=2, full lookup table, as before but renamed,
- g_v2k5.r_s (k=5)
- g_v2k6.r_s (k=6)
- g_v2k7.r_s (k=7)
for 1d, multi_value, full lookup table,
- g_v3k3.r_s (v=3 k=3)
- g_v3k4.r_s (v=3 k=4)
- g_v4k2.r_s (v=4 k=2)
for 2d/3d, kcode lookup table,
- g_v3k6.r_v (v=3 k=6)

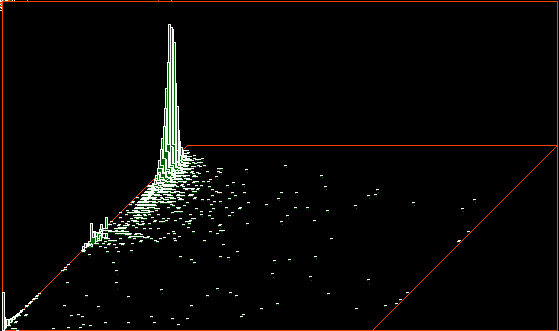
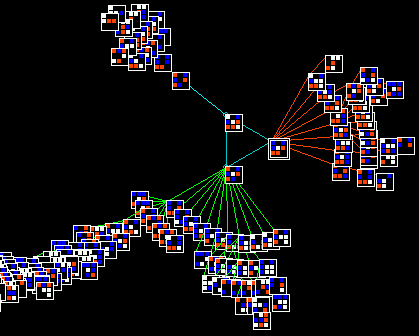
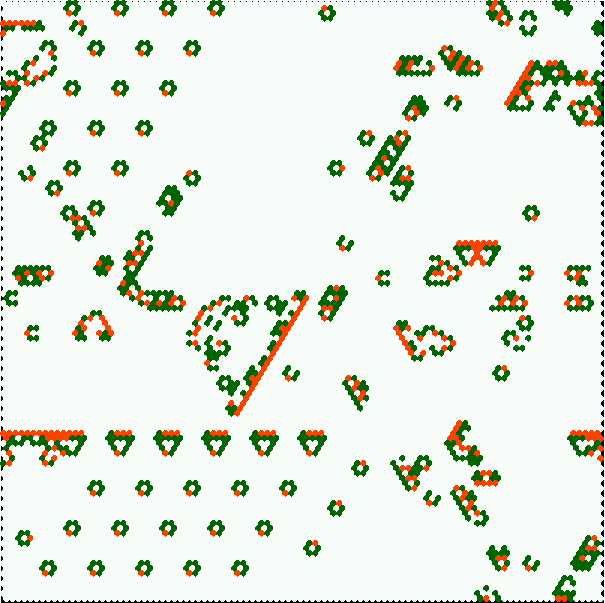
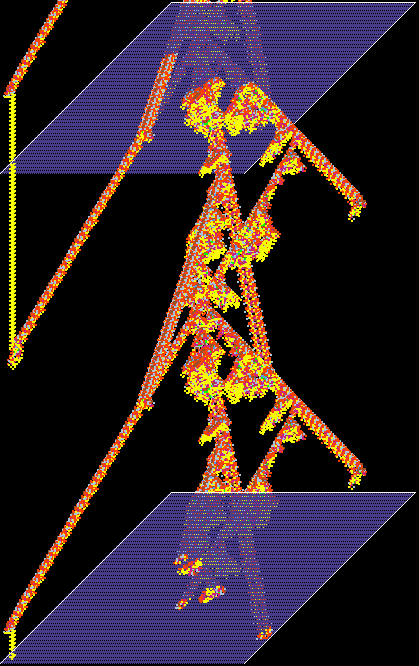
An automatically classified sample of about 16000 v=3 k=6 kcode rules for 2d hex CA
Axies are as follows:
x=standard deviation of the input-entropy, y=mean entropy, z=frequency of rules on the xy scatter plot.
Complex rules are spread out on the right with higher standard deviation, Chaotic and ordered rules are on the left with low standard deviation - chaos has high entropy (the tower), and order lower entropy.



	The "un-slant" option, rule 153, Click to enlarge.

New/revised on-the-fly options

When running forward, there are some new and revised on-the-fly options as follows:

rules

r/K/k..rnd rule/tcode/kcode: set a random rule:
- r a random rule (full lookup table).
- K a random tcode. k) a random kcode.
[/]..sym/legal: set a random rule (full lookup table).
- [ a "symmetric" rule, where 1d/2d/3d rotation symmetric neighborhoods have the same output.
- ] a "legal" rule (symmetric + "uniform"), where (mono-color) neighborhoods output that color.
O/A/M/C..Orig/Alt/Maj/Chain
- reset the original rule.
- set a random Altenberg rule.
- set a majority rule; make the output the neighborhood's majority color, if tie, pick one of the highest at random.
- set a random or chain rule.
B..flip allv->v make the current rule "uniform", as in "legal" above.

presentation

R..rearrange cell color randomly rearranges the allocation of colors to values.
i..tog divs (off) for 2d, toggle the divisions between cells.
3/./^..tog color cell/dot/bground for 2d, toggle
(3) cell color according to value/neighborhood (as before),
(.) a dot on the zero value cells,
(^) the color of the zero value cells.

change seed size

4/v/o..rnd seed/block/orig
- 4 resets the pattern, the density predefined.
- v sets a random block, the size and density predefined.
- o restores the original initial state.
5/6..singleton pos/neg for multi-value both set a cell with a random color against a
background of a different random color. For v=2 (as before) 5 sets a positive seed
(a central 1 with a background of 0s), 6 sets a negative seed.
l/L..rnd value/block
- l randomly flips the value of a cell at a random position.
- L adds a random central block, where the size of the block was defined before.

presentation

x..tog slant (off) for 1d, some CA space-time patterns are asymmetric, for example rule 60.
This option makes the space-time patterns appear symmetric.
x..tog hex (off) for 2d, toggle the 2d lattice between square and hex (discused above).
- In both cases the present status is indicated by (on)/(of).
R..rearrange cell color randomly rearranges the allocation of colors to values.
i..tog divs (off) for 2d, toggle the divisions between cells.
3/./^..tog color cell/dot/bground for 2d, toggle
(3) cell color according to value/neighborhood (as before),
(.) a dot on the zero value cells,
(^) the color of the zero value cells.

Falling of edge boundary conditions

By default, the boundary condition in DDLab are periodic, a ring for 1d, a torus for 2d and a 3d torus for 3d. There is a new option, in the top right space-time pattern interrupt options, to set a fixed border of a given value and width.

fixed border-B If B is selected, there is a further prompt,
- fixed border: width (0-25, now 0):
- border value: (0-2, now 0):

If a suitable border width, and border value (same as the background), are set, gliders and other structures in 2d and 3d complex CA can seem to fall of the edge, simulating an infinite space, though structures sometimes interact with the edge.

Scrolling 2d space-time patterns

The basic 2d pattern can be transformed on-the-fly into two different kinds of space-time patterns (axonometric projections), and both can be scrolled for a continuous view of the unfolding of the dynamical system (click to enlarge).
The system shown is a complex kcode CA on a hex lattice, with two glider guns. These glider guns oscillate between the firing of gliders in opposite directions.

above:
the basic (default) 2d presentation
right:
starting with the basic 2d presentation, enter 't' to project a vertical axonometric, as if looking up into a shaft (an old option). A new option makes the pattern scroll when reaches the bottom of the screen; enter "#" to toggle scrolling on/off.

above:
starting with the basic 2d presentation, enter "#" to project a diagonal axonometric, which will automatically scroll when it reaches the bottom of the screen; enter "#" to toggle between basic 2d and this presentation.

Reaction-Diffusion Dynamics, Excitable Media

Reaction-Diffusion dynamics [Greenberg and Hastings] is made with a CA consisting of 3 types of cell: resting, excited, and refractory. There is usually one resting type, one excited type, and one or more refractory types. A resting cell becomes excited if there is a threshold, or threshold interval (t) of exited cells within its neighborhood. An excited type changes to refractory. A refractory type changes to the next refractory type (if there are more than one) and the final refractory type changes back to resting, completing the cycle. The resulting dynamics produces waves and spirals and related patterns that can resemble the BZ reaction and other types of excitable media. The dynamics depends on the initial state and its density of non-resting types - usually low for best results. Reaction-Diffusion dynamics can also be produced with a locally wired random network, where each cell has random inputs from a local zone.

resting -(t)-> excited -> ref₁ -> ref₂ ...->... ref_n -> resting

In DDLab Reaction-Diffusion can be set as an "outer" k-totalystic rule, or as a full lookup table.

In the first method, select outer k-totalystic, as described in section Forward only for just totalistic rules

totalistic only: outertot-o/+o, tcode-t, (def-kcode): Enter o
then in a top right prompt
... ReactionDiffusion-R ...
Enter R.

As a full lookup table, at the prompt for selecting a rule, enter R (... RD-R ...). Note that max v/k allowed is smaller than with the outer k-totalystic rule method.

Reaction-Diffusion on a 222x222 hex grid k=12, v=6:
0 rest, 1 excited, 2 to 6 refractory. The threshold interval is 5 to 6. Reaction-Diffusion on a 122x122 square grid k=8, v=8: 0 rest, 1 excited, 2 to 6 refractory. The threshold interval is 1 to 6. Non-resting density about 30%

Reaction-Diffusion on a 255x255 square grid,
v=5: 0 rest, 1 excited, 2 to 5 refractory. The threshold interval is 3 to 15. k=24 random connections within a 12 cell diameter local zone.

Reaction-Diffusion on a 255x255 square grid k=11,
v=8: 0 rest, 1 excited, 2 to 11 refractory. The threshold interval is 2 to 7. k=11 random connections within a 12 cell diameter local zone.

Return to the Discrete Dynamics Lab home page.
Last modified: Sept 2005

	k=16	k=17	k=18	k=19	k=20	k=21	k=22	k=23	k=24	k=25
square lattice
hex lattice