Discrete Dynamics Lab
Update May 2002
version 24
new manual, new features
The most significant update is that the new manual is complete
(421 pages, 209 figures), and corresponds exactly
to this DDLab release, version 24.
The new version of DDLab includes many new features, functions,
improvements and revisions, both major and minor,
since the last official release
in Feb 1999. Some of these are listed below, with links to illustrations.
Changes not listed will be clear from the manual.
A number of logical, presentation and "crash"
bugs have also been fixed (and not too may added - I hope).
For previous updates since March 96, click
Feb 99 and
Sept 97.
Some new features and changes
Graph tools
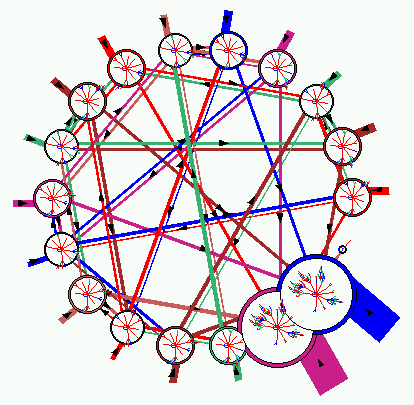
- DDLab now includes powerful graph tools which have two distinct applications.
Firstly to represent the CA or RBN network itself - the ``network graph''.
Secondly to represent the ``meta-graph'' of the basin of attraction field.
Click here for examples.
- The attractor meta-graph
represents the probability
of jumping between basins of attraction due to 1-bit perturbations to attractor
states in the the basin of attraction field.
- The network graph represents the CA or RBN network itself.
Links can be changed, added and cut within the graph, but this does not affect
the underlying network, which can be changed in the
"wiring graphic" and "wiring matrix" as before.
- Both the network graph and attractor meta-graph allow
very flexible methods for rearranging and
unraveling the graph:
- Single nodes, connected
fragments, or whole components, can be dragged with the mouse,
with ``elastic band''edges,
according to inputs and/or outputs.
- The distance of fragment links from a node
can be restricted, i.e. dragging
the node + its immediate link nodes (step 1),
the node + immediate links + their immediate links (step 2), etc.
- Predefined 1d, 2d and 3d blocks can also be dragged.
- Nodes and links can be re-scaled, and have alternative presentations.
- Unreachable or hard to reach nodes can be identified and isolated.
- Nodes with the fewest links can be automatically moved to the
outer edges. This makes it easy to unravel a graph.
- The pre-programmed graph layouts available are a circle of nodes, a
spiral, or a layout in 1d, 2d or 3d.
- The graph (or fragments) can be rotated,
flipped, expanded, contracted, "shaken",
and various other manipulations can be performed.
- The graph layout can be saved/loaded.
- An ``ant'' can be launched into the network that moves according
to the link probabilities (as in a Markov chain) keeping a count
of node hits.
- The data from which the graph is generated can be shown as a table,
called the ``adjacency matrix'' for networks,
and the ``jump-table'' for the meta-graph.
Network architecture
- The network architecture prompt has been redesigned
with a number of new options:
- Show the network as a graph as described above.
Click for examples of the same "scale free" n=50
network, in circle
layout with some nodes dragged, and
"unscrambled".
- A new wiring graphic option, the 1d circle layout,
with the same options as the
1d wiring graphic.
Click for examples:
1,
2,
and 3.
- Extra options for the wiring graphic:
- Set a "block" in 1d, 2d or 3d,
where wiring (and rule) options apply just to the block.
- Set random wiring (for the network or block) biased
according to inputs k.
If a power distribution of k
was set, this also gives a power distribution of outputs.
- The frequency of
inputs k,
outputs,
or both,
can be shown as a histogram.
- "Kill" a node, cut all output wires and input
wires, except one input to itself, then set rule 2 (i.e. no change).
- Delete a node, i.e. reduce the network by one cell
(for the 1d networks only).
Wiring, mixed-k
- When setting mixed-k, there's a new option to
set normal distribution, or a
power law distribution with a given power exponent.
Setting rule/s, new options
- Force the Z-parameter higher/lower.
- Set a chain-rule (or rules).
These are maximally chaotic rules where the degree of pre-imaging
approaches 1 with increasing system size, and G-density
approaches 0.
Attractor basins
- New mutation option, where a rule is chosen randomly
from the set of chain-rules (see above).
- When showing the actor meta-graph, the basins of attraction
can be shown within the
meta-graph nodes, or the layout
can simply follow the meta-graph node layout,
so can be rearranged in any way,
click here for
an example (k=3 rule 81, n=10).
- A new option allows single basin mutants to be
shown together on one screen, click
here for
an example.
- The RBN reverse algorithm:
a new method has been introduced that
re-orders the network to increase the wiring overlap
between successive cells.
This minimizes the growth of the partial pre-image stack, reducing
memory load and speeding computation.
The method is now the default, but can be suppressed.
The re-ordering is entirely
local within the algorithm. It should make no (or very little)
difference to the presentation of attractor basins.
The re-order is displayed below the top right window.
- Data on attractor basins can now include a complete list of
states in each basin, including the number of pre-images
and level away from the attractor.
The Derrida plot
- A new measure, the Derrida coefficient is introduced.
The Derrida coefficient is
the log of the tangent of the initial slope of the plot,
and varies between about +1.3 and -1.2, where positive values indicate
increasing chaos, negative values indicate increasing order.
Click here
for examples
Space-time patterns, various new/revised options,
and on-the-fly options, including,
- The samples of glider rules have been increased.
- New option for showing the fractal nature
of space-time patterns, the
return map
in a 2d-phase plane.
- frequency bins: As well as showing "frozen" cells
in space-time patterns,
a new function displays the frequency of 1s in window of time-steps.
Cells are shown in color according to preset "bins".
The default (and max) is 10 equal bins, but the number of bins
and bin boundaries can be revised.
- Network graph: Space-time patterns can be shown
in network graph layout at the same time as normal layout.
For example a
1d circle layout for
1d CA,
or 2d triangular layout
for 2d where k=6 or 7. Any arbitrary layout can be
implimented by rearanging the network graph.
- Probabilistic networks:
2 types of randomness can be set for space-time patterns,
``update'' probability gives some asynchronicity.
``output'' probability introduces noise.
The degrees of randomness can be set independently, and
both ``update'' and ``output'' can be set at the same time.
Return to the
Discrete Dynamics Lab home page.
Last modified: July 2001