var_to_autocov
Return autocovariance sequence for a VAR model
Syntax
[G,info] = var_to_autocov(A,SIG,acmaxlags,acdectol,aitr,maxiters,maxrelerr)
Arguments
See also Common variable names and data structures.
input
A VAR coefficients matrix SIG residuals covariance matrix acmaxlags maximum autocovariance lags to calculate or (default) zero for automatic calculation acdectol autocovariance decay tolerance (default: 1e-8) aitr use "accelerated iterative" Lyapunov solver algorithm, else (default) a Schur algorithm (see Description) maxiters maximum iterations if using iterative algorithm; see 'dlyap_aitr' for defaults maxrelerr maximum relative error if using iterative algorithm; see 'dlyap_aitr' for defaults
output
G autocovariance sequence
info info structure, with fields (some may not be present):
error error number (0 if no error)
errmsg error message string
warnings number of warnings (0 if no warnings)
warnmsg warning mesage strings (cell array)
rho VAR spectral radius
iters number of iterations if using iterative algorithm, else 0
acrelerr relative error of associated 1-lag solution
acminlags minimum lags required to achieve specified autocovariance decay factor
aclags actual number of autocovariance lags calculatedDescription
Returns autocovariance sequence G defined as 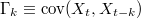 for a VAR model with coefficients A and (positive-definite) residual covariance matrix SIG, by "reverse-solving" the Yule-Walker equations
for a VAR model with coefficients A and (positive-definite) residual covariance matrix SIG, by "reverse-solving" the Yule-Walker equations
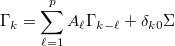
(where  = SIG). The algorithm solves the associated 1-lag problem - a discrete-time Lyapunov equation - and then calculates higher lags recursively [1].
= SIG). The algorithm solves the associated 1-lag problem - a discrete-time Lyapunov equation - and then calculates higher lags recursively [1].
Errors, warnings and diagnostics are returned in the info struct. Use the routine var_info (which should always be called after this function) to display this information. Possible errors are
info.error info.errmsg
----------------------------------------------------------------------
0 (no error, no message)
1 unstable VAR (has unit root)
2 residuals covariance matrix not positive-definite
3 Lyapunov equation solver failed for some reason
4 1-lag residuals covariance matrix not positive-definite
----------------------------------------------------------------------For a stable VAR the the spectral radius info.rho (see var_specrad) must be < 1; this may be considered a unit root test for stationarity [1]. Then the autocovariance sequence decays approximately exponentially, by a factor equal to info.rho. The minimum number of lags required to achieve the specified autocovariance decay tolerance acdectol is calculated as info.acminlags, so that info.rho^info.acminlags < acdectol. The actual number of lags info.aclags to which autocovariance is calculated is then set to the minimum of info.acminlags and the specified maximum number of lags, acmaxlags (if acmaxlags is not supplied - the recommended option - it defaults to info.acminlags). A warning is issued if info.aclags < info.acminlags. In this case there is no guarantee that MVGCs - particularly in the spectral domain - will be accurate. However, if the spectral radius of the VAR model is close to 1, so that info.acminlags is unfeasibly large, there may be no alternative [note that most Granger causality libraries effectively set info.aclags to the model order]. The calculated 1-lag autocovariance matrix is also checked for positive-definitiveness. If this check fails, it may be an indication of an ill-conditioned VAR (possibly because residuals variances are too small, and/or the process is borderline stationary). In short, the info.error field must be checked by the caller: 0 signifies success, > 0 signifies an error with corresponding message in info.errmsg. Attention should also be paid to any warnings in info.WARNINGn.
The aitr flag specifies a fast (but experimental) "accelerated" iterative Lyapunov solver algorithm (see dlyap_aitr). If not set (default), the Control System Toolbox dlyap solver routine is used if available, else a roughly equivalent (but slower) scripted algorithm based on Schur decomposition (see dlyap.m in the utils/control directory).
References
[1] L. Barnett and A. K. Seth, The MVGC Multivariate Granger Causality Toolbox: A New Approach to Granger-causal Inference, J. Neurosci. Methods 223, 2014 [ preprint ].
[2] X. Kitagawa, An algorithm for solving the matrix equation X = F X F'+S, Internat. J. Control 25(5), 1977.
[3] S. Hammarling, "Numerical solution of the stable, non-negative definite Lyapunov equation", IMA J. Numer. Anal. 2, 1982.
See also
var_specrad | var_info | dlyap (ControlSystem Toolbox) | dlyap (scripted Schur algorithm) | dlyap_aitr