dlyap
Solve discrete-time Lyapunov equation by Schur decomposition
Syntax
X = dlyap(A,Q)
Arguments
See also Common variable names and data structures.
input
A square matrix with spectral radius < 1 Q symmetric positive-definite matrix
output
X solution of discrete-time Lyapunov equation X = A*X*A'+Q
Description
Solves the discrete-time Lyapunov equation
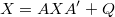
using Schur decomposition and column-by-column solution [1,2] (this is quite likely the same algorithm as in the Matlab Control System Toolbox dlyap, except that no balancing is performed). This function is substantially slower than dlyap; if the Matlab Control System Toolbox is not available, the user might like to consider using dlyap_aitr instead.
The caller should test that Q is positive-definite and that the spectral radius of A is < 1 before calling.
Adapted from an early scripted (i.e. non- SLICOT) version of Octave's dlyap function.
References
[1] X. Kitagawa, "An algorithm for solving the matrix equation X = F X F'+S", Internat. J. Control 25(5), 1977.
[2] S. Hammarling, "Numerical solution of the stable, non-negative definite Lyapunov equation", IMA J. Numer. Anal. 2, 1982.