dlyap_aitr
Solve discrete-time Lyapunov equation by Smith's accelerated iterative method
Syntax
[X,iters] = dlyap_itr(A,Q,maxiters,maxrelerr)
Arguments
See also Common variable names and data structures.
input
A square matrix with spectral radius < 1 Q symmetric positive-definite matrix maxiters maximum iterations (default: 100) maxrelerr maximum relative error (default: 1e-8)
output
X solution of discrete-time Lyapunov equation X = A*X*A'+Q iters number of iterations performed
Description
Solves the discrete-time Lyapunov equation (cf. dlyap in the Matlab Control System Toolbox)
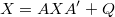
using Smith's accelerated iterative method [1]:
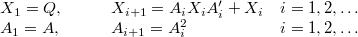
maxiters is the maximum iterations, maxrelerr the maximum relative error of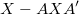 
with respect to Q before a convergence test kicks in. The actual number of iterations performed is returned in iters. If the algorithm fails to converge within maxiters iterations, an exception MVGC:XMaxItrs is thrown (this is for consistency with dlyap). The convergence rate depends on the problem dimensions and maximum absolute eigenvalue (spectral radius) of A. In general this algorithm actually appears to be faster than the Matlab Control System Toolbox dlyap.
The caller should test that Q is positive-definite and that the spectral radius of A is < 1 before calling.
References
[1] R. A. Smith, "Matrix Equation XA + BX = C", SIAM J. Appl. Math. 16(1), 1968.