autocov_to_var
Calculate VAR parameters from autocovariance sequence
Syntax
[A,SIG] = autocov_to_var(G)
Arguments
See also Common variable names and data structures.
input
G autocovariance sequence
output
A VAR coefficients matrix SIG residuals covariance matrix
Description
Calculates regression coefficients A and residuals covariance matrix SIG from the autocovariance sequence G defined as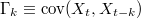 
by solving the Yule-Walker equations
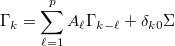
(where 
= SIG). For a q-lag autocovariance sequence, this routine corresponds to an autoregression of q lags. It also effects an efficient spectral factorisation if called with the autocovariance sequence derived from the cross-power spectral density (e.g. as calculated by cpsd_to_autocov).
This routine implements Whittle's recursive LWR algorithm [2] which, for n variables, performs 2q separate n x n matrix inversions as compared with a single nq x nq matrix inversion for the conventional "OLS" solution of the Yule-Walker equations (see [1]). The LWR algorithm also (unlike OLS) guarantees that if the "true" regression model is stable, then the estimated model is also stable, even if not of the correct order.
Note: If the regressions are rank-deficient or ill-conditioned then A may be "bad" (i.e. will contain a NaN or Inf; see isbad) and/or warnings will may be issued. The caller should test for both these possibilities, by calls to isbad and warn_supp ... warn_test respectively. The likely cause is that something went wrong in var_to_autocov, which is typically called prior to this function; check the results of the latter with a var_info call.
References
[1] L. Barnett and A. K. Seth, The MVGC Multivariate Granger Causality Toolbox: A New Approach to Granger-causal Inference, J. Neurosci. Methods 223, 2014 [ preprint ].
[2] P. Whittle, "On the fitting of multivariate autoregressions, and the approximate canonical factorization of a spectral density matrix", Biometrika, 50, 1963.
See also
var_to_autocov | cpsd_to_autocov | warn_supp | warn_test | isbad | var_info