GCCA_tsdata_to_pwcgc
Calculate pairwise-conditional time-domain MVGCs (multivariate Granger causality) from time series data by "traditional" method (as e.g. in GCCA toolbox)
Syntax
[F,A,SIG,E] = GCCA_tsdata_to_pwcgc(X,p,regmode)
Arguments
See also Common variable names and data structures.
input
X multi-trial time series data x vector of indices of target (causee) multi-variable y vector of indices of source (causal) multi-variable p model order (number of lags) regmode regression mode (default as in 'tsdata_to_var')
output
F Granger causality matrix A VAR coefficients matrix SIG residuals covariance matrix E residuals time series
Description
Returns the matrix F of pairwise-conditional time-domain MVGCs
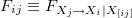
(where [ij] denotes omission of the ij-th variables) between all pairs of variables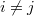 
represented in G, for a stationary VAR process with autocovariance sequence G. Note that the first index i of F is the target (causee) variable, the second j the source (causal) variable. See ref. [1] for details. The regression mode is set by the regmode parameter, which may be 'LWR' or 'OLS' (see tsdata_to_var for details and defaults). The VAR parameters A,SIG and residuals E of the full regression are (optionally) returned.
If p is a scalar, p lags are used for both the full and reduced regressions. Otherwise, if p is a vector of length 2, then p(1) is the number of lags for the full regression and p(2) the number of lags for the reduced regression (note: this is generally a bad idea! - see the accompanying documentation [1] for reasons).
The caller should take note of any warnings issued by this function and test results with a call isbad|(F,false)|.
This routine is included mainly for compatibility with the Granger Causal Connectivity Analysis (GCCA) Toolbox [2]; the MVGCs are calculated by performing separate full and reduced regressions - see [1] for details and mvgc_demo_GCCA for example usage. Note that the preferred MVGC Toolbox method of calculating MVGCs via the autocovariance sequence (see autocov_to_pwcgc, mvgc_demo) only requires a single regression step and are thus generally more accurate.
References
[1] L. Barnett and A. K. Seth, The MVGC Multivariate Granger Causality Toolbox: A New Approach to Granger-causal Inference, J. Neurosci. Methods 223, 2014 [ preprint ].
[2] A. K. Seth, "A MATLAB toolbox for Granger causal connectivity analysis", Journal of Neuroscience Methods 186, 2010.
See also
GCCA_autocov_to_mvgc | autocov_to_pwcgc | tsdata_to_var | mvgc_demo_GCCA | isbad