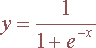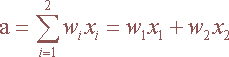MTCS Tutorial 1

MTCS Tutorial 1 : Matlab and Neural Network Basics

Matlab basics.

Matlab script language provides you with all the basic elements of a standard programming language plus a variety of build-in structures and functions that make programming easier but slower than with other languages. Therefore it is very useful for designing prototypes.

Like any other language, Matlab supports the basic mathematic calculations, variables, logical operators etc. The best way to get around Matlab is by using the Helpdesk and the help function. You can access on-line the complete manuals, if you need more information. You can also find Matlab Tutorial books in the University Library.

Matlab supports logical operation functions such as AND OR NOT XOR.

Matlab supports the following control structures:

if statements
switch statements
for loops
while loops
break statements

Matlab would not be quite as useful without the ability to write programs. Programs in Matlab have to end with .m e.g. myprogram.m and are called M-files. You may write them by using the editor of your preference.

There are generally two types of M-files, scripts and functions. Scripts are just plain files that include Matlab commands (fig 1). It is useful to put all the variables at the beginning of the file, in order to edit them easily before a rerun of the program to get new results.

script sample

Functions have a specific structure and it is preferable to store them in a file with the same name as the function name. If figure 2 you can see a simple function example.

function sample

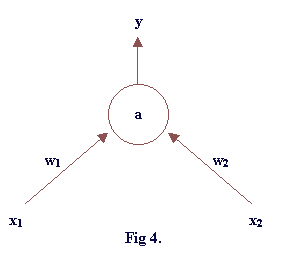
You should either use addpath to make Matlab look in the directory where you are going to develop your program or simply make sure that you can see your program when you give the ls command at the Matlab prompt. If not you can use the cd command to go to directory where you keep your files. To run a script or a function, simply type at the Matlab prompt its name (including the arguments in case of a function).

Neural Network Basics.

Consider that we have a single neuron unit that receives an input x. The activation of the neuron (a) is simply the result of multiplying the input with a weight w : a=w*x. The output of the neuron, which we will call y, can be set equal to the activation (y=a, linear case), but quite often the activation is used as an input to another function, usually sigmoid or step function. In the latter case, the output of this function is the network output y.

single neuron unit

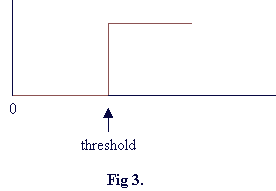
A step function has output 1 if the input is greater than a specific number (threshold) and zero elsewhere (fig 3).

step function

A sigmoid function has the form:

sigmoid function

which is the same as y=1/(1+exp(-x)). Here is a simple example of a single neuron implementing the logical function AND. The network has the following structure (fig4):

AND

where x₁,x₂ are the inputs of the network, w₁, w₂ the weights and a the activation of the node. The activation is is calculated by the expression:

nn output

In general, there is a procedure for the network to learn the appropriate weights, but for a start we will take for granted that w₁=1 and w₂=1.

In this case the activation of the neuron will be used as input to the step function. For a threshold value 2 the network result will be the logical function AND of its two inputs x₁ and x₂. It is easy to understand why this is true. The following table shows the desirable behaviour of the network:

Input sets x₁ x₂	Output t
0 0	0
0 1	0
1 0	0
1 1	1

For w₁=w₂=1, we calculate the activation for each of the cases above. The larger value is when both inputs are 1 (a=2). If one input equals to 1 and the other equals to 0, the activation a becomes 1. Chosing a value for the threshold of the step function that is greater than 1 and smaller than two 2, the network output becomes 1 only if both inputs are equal to 1.

[ Main Page | Tutorial 1 | Tutorial 2 | Tutorial 3 ]