Maths Tools for Cognitive Scientists Lab 3 (Week 4)

Part a

http://www.informatics.sussex.ac.uk/users/bg22/mtcs/mtcs3a.html

1. Create matrices in matlab (type the text between angled brackets):
   • Use a built-in matlab function:

     < o = ones(5,3) > creates a matrix of 1's with 5 rows and 3 columns.

     NB: An m x n matrix has m rows and n columns. (Rows first, then columns.)

     < r = rand(4,4) > creates a matrix of random numbers with 4 rows and 4 columns.

   • Enter an explicit list of elements using square brackets [ ]:

     < m1 = [2 3 4] > creates a matrix with 1 row and 3 columns.

     < m2 = [5; 6; 7] > creates a matrix with 3 rows and 1 column (the semicolon separates the rows).

     < m3 = [1 1; 3 3; 5 5] > creates a matrix with 3 rows and 2 columns.

   • Load a matrix from a space- or tab-delimited file:

     Type the following into the editor (use spaces or tabs between the numbers) -

     16     3     2    13
      5    10    11     8
      9     6     7    12
      4    15    14     1

     
     Save this as a file called magic1.dat and load it into matlab using the command

     < load magic1.dat >

     The matrix will now be in your workspace, type < magic1 > to see it.

    

2. Matrix scalar multiplication (and division):

   Every entry of the matrix is multiplied separately by the scalar.

   
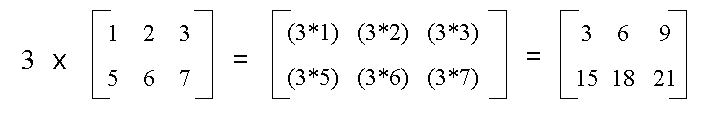
   Multiply the matrix < m3 > by 4 and call it < m4 >.

   Divide < m4 > by 2.

 
3. Element-by-element multiplication (,division and raising to a power):

   The elements of each matrix are multiplied by the corresponding element in the other matrix
   which must have the same shape.

   • Use the < .* > notation to multiply element-by-element the < magic > matrix and the
     < r > matrix (they should be in your workspace).

   • Create a 4x4 matrix of ones and multiply it by the scalar 8 - call it < m5 >.

   • Make a new matrix < m6 > by doing the element-by-element cube root on < m5 >.
     (Hint - to get the square root you raise to the power 1/2.)

   • Make a new matrix < halfmagic > by doing element-by-element divide < magic1 > by < m6 >.

 

4. Matrix multiplication:

   Two matrices can only be multiplied if the number of columns in the first is equal to the
   number of rows in the second.

   If matrix A has m rows and n columns: A_(m,n)
   and matrix B has n rows and p columns: B_(n,p)
   then their product, matrix C, has m rows and p columns: A_(m,n) x B_(n,p) = C_(m,p)

   Each element in the first row of A is multiplied by the corresponding element in the
   first column of B and the products added to give the first element of C:

   c₁₁ = (a₁₁*b₁₁ + a₁₂*b₂₁ + a₁₃*b₃₁ + ... a_1nb_n1)

   Similarly, the next element of C in the first row is given by the sum of the products
   of the elements in the first row of A and the second column of B.

   

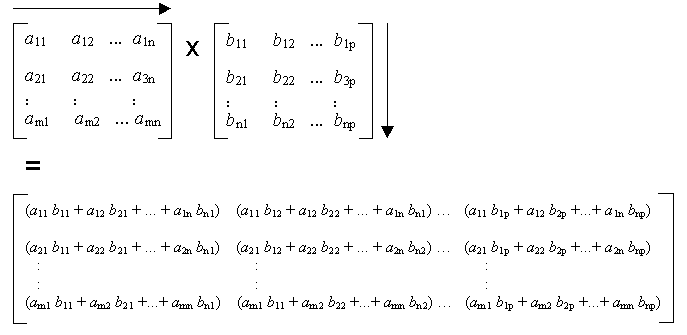
   For example:

   

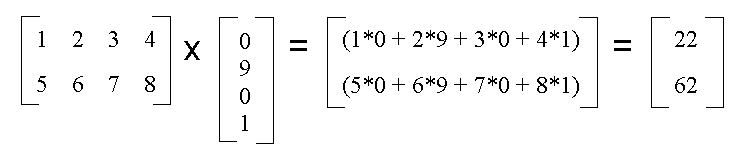
   On paper, try multiplying the following pairs of matrices.
   Then check if you are correct using matlab.

   

   

    

 

5. Subscripts: accessing elements of matrices:

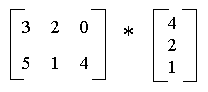
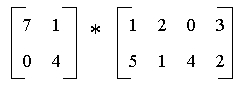
   To access an element in row 3 and column 2 of matrix A type < A(3,2) >.

   • Use the colon operator < : > to access the first column of the matrix < magic1 >.
   • What is the element in row 3, column 5 of the matrix < o > in your workspace?
   • Use the colon operator and the empty matrix < [] > to delete the last row of < r >.

 
6. Some functions that can be used on matrices:

   < sum >	sums the elements of a matrix column-wise
   < rot90 >	rotate a matrix by 90—
   < flipud >	flip matrix upside-down
   < fliplr >	flip the matrix left-right
   < diag >	extracts matrix elements on the main diagonal (top left to bottom right)

   • In matlab the transpose of a matrix A is denoted by A'. What is the transpose of the
     magic square < magic1 > ? How does it relate to the original matrix?
   • Calculate the column-wise sums of the matrix < magic1 > and its transpose.
   • Find the sum of the elements on the main diagonal of < magic1 >.
   • What then are the properties of a magic square?

    

Now go to Part b