The area of probability and statistics is an enormous one with vast applicability. This teach file summarises, in sketchy outline, a few of the more basic and useful topics in this field.
Mathematically, a probability is a number between 0 and 1, which is manipulated according to certain rules, and these are well established and well understood. The interpretation of probabilities remains, however, a matter for debate. Very roughly, there are two schools of thought. For the frequentist school, the probability of an event is the fraction of times that the event will occur if the situation leading up to the event is replicated as exactly as possible. For the subjectivist school, the probability of an event is a measure of the strength of belief of a rational being that the event will occur. Whilst these differences are important both at a philosophical and practical level, they will be left to one side here.
In classical physics, probabilities reflect ignorance on the part of an observer (we express the fall of a coin in terms of a probability because we do not know enough about the exact spin, lift etc. imparted when it is tossed), whilst in quantum physics the uncertainty entailed in the use of probabilities is a fundamental property of nature (the future state of an atomic particle cannot, even in principle, be predicted exactly). In Artificial Intelligence, probabilities are generally used to deal with the ignorance of a reasoning system about the exact details of a situation. In simulation studies, probabilistic reason is used both to set up initial conditions and to interpret the outcomes of repeated trials.
Textbooks such as that by Boas (see FCS1) give an introduction to probability. The use of probabilities will be encountered in almost every branch of the study of evolutionary and adaptive systems.
The probability of an event E is written P(E), or sometimes as Pr(E). For example, if H is the event that a tossed coin turns up heads, and the coin is fair, then we might write P(H) = 0.5.
A fundamental property of probabilities is that if two events A and B are mutually exclusive (i.e. they cannot both occur), then
P(A or B) = P(A) + P(B)
(Notation: where I have used the word "or", books often use a symbol like a U, which also means set union, or a symbol like a v as in predicate calculus.)
For example, P(H) = 0.5 and P(T) = 0.5, and H and T cannot both occur (perhaps because they stand for heads or tails in a single coin toss), then P(H or T) = 1.
This last example illustrates another fundamental property: if a set of events is complete (i.e. one of the events in the set must occur) and all the events are mutually exclusive, then their probabilities add up to 1. It is occasionally helpful to think of probability as a limited resource which has to be distributed over the possible events in a way which reflects how likely each one is.
More formally, if events X[1] ... X[N] are complete and mutually exclusive (i.e. exactly one of them must occur), then
SIGMA P(X ) = 1
i i
In fact, what I have said so far is sufficient to establish the formal basis of probability theory. One consequence of these properties is that if A and B are two events that are not necessarily mutually exclusive, then
P(A or B) = P(A) + P(B) - P(A and B)
where "A and B" means that both events happen. (This is often written A & B, or using an inverted U (set intersection) or inverted v symbol. You may also see P(AB) and P(A,B), meaning the same thing.) The formula makes sense, in that if the two events are mutually exclusive, then P(A and B) = 0, giving the previous formula.
Textbooks (e.g. Boas - see FCS1) devote a large amount of space to the matter of estimating the probabilities of different kinds of event. Such questions as "What is the probability that you and a friend have different birthdays?" are the grist to this mill, which also involves a lot of throwing of dice and drawing of cards.
Questions like this generally involve summing probabilities for mutually exclusive events. A sample space of all possible mutually exclusive primitive events is set up; usually there is some symmetry argument that makes the probabilities for all these events equal. Then primitive events have to be combined to create the set of circumstances that allows the question to be answered; the probabilities for the primitive events are summed. Although this sounds simple, subtle and complex arguments are often needed to get it right.
As this is standard textbook material, I will not dwell on it. Here is a simple example, just to give the general idea. Suppose that in some genetic code strings of length 5 are generated by randomly selecting from the characters A, B, C and D with equal probability. What is the probability of finding the combination AAAA somewhere in a given string? First, the sample space is the space of all possible strings (AAAAA, AAAAB, AAAAC etc., to BDDDD, CDDDD, DDDDD). Each of these has the same probability, and there are 4^5 of them. The probability of each one is 1/4^5, or approximately 0.001. 4 of the strings have AAAA at the left end, and 4 have AAAA at the right end, but AAAAA is common to both these groups, so the total number containing AAAA is 7. Thus the probability required is 7/4^5 or about 0.007. This process of effectively counting the number of ways to get a given observation is the basis of combinatorial probability computations.
(The general case of finding the probability of a given pattern in a random string is covered by a variety of formulae depending on the exact circumstances - textbooks will give great detail when needed.)
Another way to do the example is simply to generate all the possible strings and count the number of them containing the sequence AAAA, dividing by the total number to get the exact probability. Another way is to use a Monte Carlo method, generating strings at random and estimating the probability by counting those that have AAAA. Such techniques are valuable fallbacks when textbook methods cannot be applied. Many simulation experiments are, in a sense, just Monte Carlo probability estimations.
It is often useful to talk about the probability of one event, given that another event is known to have occurred. For example, for an autonomous robot, it may be useful to consider the probability that there is a particular object - say an apple - in front of its camera, given that the robot's perceptual system is reporting the presence of a particular image feature - say a circular shape. Such a probability is a conditional probability. If A is the event that an apple is present, and C is the event that a circular shape has been detected, we write
P(A | C)
to mean the probability of there being an apple when a circular shape has been seen.
One way of thinking about this is to use a possible worlds model for probabilities. P(A) means the fraction of all possible worlds in which there is an apple in front of the camera. P(C) means the fraction of all possible worlds in which a circle is detected. P(A | C) means the fraction of worlds in which there is an apple, but considering only those possible worlds in which a circle has been detected. Whether you like a "possible worlds" way of thinking about probabilities is partly a question of your philosophical stance.
Some books use the notation
P (A)
C
to mean the same as P(A | C).
It seems reasonable that event C does tell the robot something about event A. Consider event B, which is the presence of an apple on a tree in the garden. Knowing C does not tell the robot anything about the likelihood of B. It seems reasonable to express this by writing
P(B | C) = P(B)
This formula is actually one definition of statistical independence. If the probabilities for B and C obey this rule, then B and C are statistically independent. It is often useful to assume statistical independence between variables even when this is not strictly justified.
One warning - unnecessary I hope. If two events really are physically independent, then they will be statistically independent and observing one of them will not affect the probability of the other. Failing to realise this is the classical gambler's error. Observing six heads in six tosses of a coin does not mean that the probability of a head on the next toss is anything other than a half, provided the coin is fair. It is easy for subtle versions of this error to crop up, and it is advisable to watch out for them. (The chairman of the National Lottery was quoted in a newspaper as saying that high numbers had a good chance in a particular week because there had been a preponderance of low numbers before that - one might have hoped that someone in his position would have known better.)
There is a second way to express statistical independence numerically. If B and C are independent, then the probability of both events occurring is given by
P(B and C) = P(B) * P(C)
This can be shown to be equivalent to the definition above in terms of conditional probability. It is an important relationship, in that it is often useful to assume that different events are independent, because we know of no causal link between them, and to work out probabilities of combinations of events using this product rule.
There is a very important relationship concerning conditional probabilities. We will approach this by putting some numbers into the perception example above.
Suppose that the robot "knows" that apples happen to be in front of its camera on one-tenth of the occasions that it looks, so
P(A) = 0.1
and that it detects a circular shape in the image on one-fifth of the occasions that it looks, so
P(C) = 0.2
In addition, the robot knows from previous experience (when it has been shown something and told that it definitely is an apple), that it detects a circular shape three-quarters of the time when an apple is in front of it. That is,
P(C | A) = 0.75
Now the robot, roaming its world in search of food, detects a circular shape. What is the chance that an apple is in front of it? In other words, given the data above, what is P(A | C)?
This can be answered by considering how often there is an apple in front of the camera, and the robot sees a circular shape; that is P(A and C). It is easy to work this out: an apple is in front of it one tenth of the time, and on three-quarters of those occasions a circle is seen, so the answer is three-quarters of a tenth or 0.075. In symbols
P(A and C) = P(A) * P(C | A) = 0.1 * 0.75 = 0.075
Now we know that the robot has seen a circle. The probability that there is also an apple present, given the circle, is the fraction of times an apple and a circle occur together, divided by the fraction of times a circle occurs without regard to the apple. In symbols
P(A | C) = P(A and C) / P(C) = 0.075/0.2 = 0.375
So the answer is 0.375 or three-eighths. One way of saying this is that the evidence of the visible circle has increased the probability of the hypothesis that an apple is in front of the camera from 0.1 to 0.375.
If this is unfamiliar, work through the argument again using different numbers and a different example. For instance, imagine a patient going to a doctor. M might be the event that a patient has meningococcal meningitis (with say P(M) = 0.00002, or one in 50,000), S might be the event that the patient has headache with fever (with say P(S) = 0.004, or one in 250), and it is known that patients with this kind of meningitis display headache with fever half the time (so P(S | M) = 0.5). If a patient turns up with this pair of symptoms, what is the chance that he or she has meningococcal meningitis - what is P(M | S)? (On these data, it is 0.00025 or one in 400 - but check that you get the same answer. These numbers are made up and may not correspond to reality.)
Given the numerical examples, it is possible to see how they generalise and so to write down the formula for the general case. This is Bayes' Theorem:
P(B | A) * P(A)
P(A | B) = -----------------
P(B)
Terminology: P(A) is known as the prior probability of event A - prior, that is, to knowing that B has occurred. P(A | B) is the posterior probability of A.
The theorem itself is uncontentious: it follows directly from the fundamental properties of probabilities. Extremely contentious, though, are its interpretation and its application in practice. Very often, the use of the theorem is associated with the philosophical stance which interprets probabilities as measures of strength of belief; hence "Bayesian inference" is a phrase with connotations well beyond the mere use of the formula.
The greatest practical problem with Bayesian inference is the estimation of the prior probability P(A). Usually, the conditional probability P(B | A) is estimated from some kind of experiment (or, equivalently, as part of a learning process in an a-life system), and P(B) is just a normalising factor to make all the probabilities for the alternatives outcomes to A add up to 1. The prior is much harder to estimate - if there is nothing else to go on, all the possibilities are given equal prior probalities, but this can be hard to justify, and causes technical problems when the outcome A, rather than being a definite event, is one of a continuum of possibilities, as when an estimate is being made of a real-valued number.
Nonetheless, Bayes' Theorem is well worth remembering, partly for the insight it gives into the meaning of conditional probabilities. It is of increasing importance in AI - for example, expert systems that used ad hoc measures such as confidence factors are giving way to those based on Bayesian methods. The approach has received impetus from the work of Judea Pearl, who has described algorithms for efficiently propagating probabilities through a "belief network" using Bayesian rules.
There is a second formula that is useful involving conditional probabilities. It is an extension of the basic summation relationship for probabilities of mutually exclusive events. If X[1] ... X[N] is a complete set of mutually exclusive events, and A is some event that depends on them, then
P(A) = SIGMA P(A | X ) * P(X )
i i i
This follows because the expression being summed is equal to P(A and X[i]). This is one of a set of mutually exclusive events, and if any one of them occurs, then A occurs, so the probability of all of them added together is the probability of A.
This is yet another weighted sum, and so gives another interpretation to the action of a linear neural network unit (FCS2). The weights on such a unit can sometimes be sensibly regarded as representing the conditional probabilities of event A given different input events X[i]. The input data represent the probabilities of the different events, and the output is the probability of A. Such an interpretation can only be applied straightforwardly, of course, if all the signals are in the range 0-1 and both weights and inputs are normalised to sum to 1.
Like an ordinary variable, a random variable can take any one of a set of values. For a random variable, the values represent a complete set of mutually exclusive events, and there is a probability associated with each event. The probability distribution for a random variable is just the association of a probability with each of its possible values.
For a finite set of values, this is straightforward. If X is a random variable whose values are h (for heads, perhaps) and t (for tails), then a typical probability distribution might be P(X = h) = 0.5 and P(X = t) = 0.5. This is an example of a discrete distribution.
If the random variable X can take on any of a continuous set of values - for example, if X represents any real number in the range 0 to 1 - then we have a continuous distribution and the assignment of probabilities needs some extra formalism. One way to handle this is to describe the distribution by using the probability that X is less than some particular value:
P(X < x)
where X is the random variable and x is some specific value that it might or might not exceed. This probability is a function of x - we might write it as F(x) where F is the name of the function - and is called the cumulative probability distribution.
For example, if X is equally likely to have any value between 0 and 1, then its cumulative probability is given by F(x) = x. This distribution is called a uniform distribution.
The cumulative probability does not seem to tell us the probability of X having any particular value. In fact, there is no answer to that question for a continuous variable; the nearest approach is to consider the probability that X lies within a range of values, from say x to x + delta x, or
P(X >= x and X < x + delta x)
We then consider what happens when delta x is made smaller and smaller. Assuming that the cumulative probability varies sufficiently smoothly with x, we would expect that when delta x is sufficiently small, the probability for a range of values will be proportional to the size of the range, and we expect that, approximately,
P(X >= x and X < x + delta x) = f(x) * delta x
where f(x) is some function of x. We expect that the approximation will be exact when delta x is reduced to be infinitessimally close to zero. The function f(x) is called a probability density function, and bears the same relation to probability that the density of a substance does to mass. You need to multiply a density by a volume to get a mass, and you need to multiply a probability density by the size of part of sample space to get a probability.
There is a relationship between the cumulative distribution and the probability density; it is
f(x) = d F(x) / d x
(and the cumulative distribution is the integral of the density).
Sometimes the notation p(X) is used to indicate the probability density function of a random variable X.
There is, again, a large literature on specific distribution functions. By far the most common (apart possibly from the uniform distribution) is the Gaussian or normal distribution, for which the probability density function is
1 (x - mu)^2
f(x) = ------------------ * exp( - ----------- )
sigma * sqrt(2*pi) 2 * sigma^2
where mu and sigma are called the mean and standard deviation respectively of the distribution. (The ^2 means "squared".)
The graph of this function is sometimes called the bell shaped curve. It is particularly beloved by psychologists and social scientists; so much so that a recent highly controversial book on IQ took "The Bell-Shaped Curve" as its title.
There are two reasons why this distribution is so common: one is a theoretical result which says that if a random variable is the sum of a large number of other random variables with their own arbitrary distributions, then it will tend to have an approximately Gaussian distribution; the other is that Gaussian-distributed random variables have some properties that make them easy to manipulate.
Any standard textbook will discuss this distribution, along with various other important distributions. Statistics books nearly always have a table of its values, and also a table of the corresponding cumulative distribution F(x). This is is called the error function (abbreviation erf) and is important for some statistical tests. Some mathematical software packages include a procedure for computing erf.
The bell shaped curve for the particular case of mean = 3 and standard deviation = 2 appears below as an example.
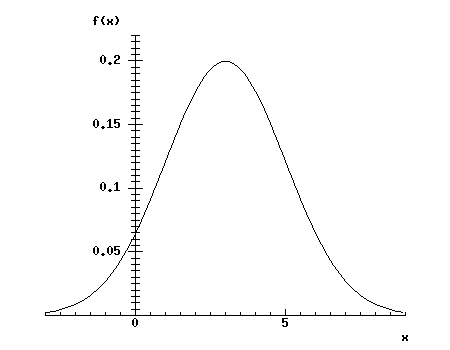
It is often necessary to summarise the distribution of a random variable using a few numbers. This might be because the exact details of a distribution are not known, or because only some of its properties are relevant to a situation. The quantities that summarise a random distribution are called its parameters, particularly when they appear explicitly in the formula for the distribution. Often, however, a distribution is not fully specified theoretically, but some aspects of it must be estimated from some data. Quantities that help describe a distribution and which have been calculated from data are called statistics. The process of estimating parameters from statistics is called statistical inference.
Here we look briefly at a few of the more important statistics. Statistical inference in general is too large a topic to embark on here, but the use of averages to describe properties of data is something that everyone should be familiar with.
One of the most important descriptors of a distribution is its mean. This term is used in two ways. In the formula for the Gaussian distribution, the mean was one of the parameters (and was denoted by mu). On the other hand, the mean is also a statistic, obtained by adding together a set of observed numbers and dividing by the number of observations. The mean is also called the arithmetic average, or just average. In the case of a Gaussian distribution, this statistic is a good estimator of the parameter mu.
It is useful to define the mean for any distribution, whether or not it appears as an explicit parameter. For a discrete distribution with a finite number of values of the variable, the mean is
SIGMA x * P(X = x )
i i i
where X is the variable, and its possible values are x[1], x[2] etc. This is often abbreviated to
SIGMA x * P(x )
i i i
where x[i] is a shorthand for the event X = x[i].
This makes sense in terms of the mean as a statistic. If we make a large number of observations, say N, we expect each x[i] to occur about N * P(x[i]) times (from the meaning of probability). Thus if we average the observation values, adding them and dividing by N, we expect to get approximately the result
SIGMA x * N * P(x )
i i i
---------------------
N
which is just the distribution mean. For this reason, the mean of a distribution is sometimes called its expectation (especially in quantum mechanics).
The mean of the distribution of a variable X is often written
__
<X> or X
Angle brackets will be used here.
The idea of an average can be extended to any numerical function of a random variable. For a function f, the general formula is
<f(X)> = SIGMA f(x ) * P(x )
i i i
In a cellular automaton, for example, the different states might be labelled with a set of symbols. An energy might be defined for each state; the average energy (which is important in some analyses) would then be obtained using a formula such as that above, if the probability of each state was known or could be estimated.
For continuous variables, the sums in the formulae above become integrals.
The mean of a distribution says, loosely, something about where its centre is. The next most useful thing to know is how spread out the distribution is. One way to measure this is to work out the average distance of the values from their mean. In practice, squaring the differences between the values and the mean not only avoids negative numbers, but makes various calculations simpler. The average squared distance from the mean is called the variance, and its formula is given by
2
Var(X) = SIGMA (x - <X>) * P(x )
i i i
It is not difficult to show that this is equivalent to
2 2
<X > - <X>
which gives a quick way to estimate the variance from data.
The square root of the variance is called the standard deviation. It turns out that if the sum above is replaced by an integral and applied to the Gaussian distribution, the standard deviation as defined here is just the parameter sigma, justifying the use of the term in the description above.
A final average that is often of great interest is minus the average of the logarithm of the probabilities of a distribution. This is at first sight a strange thing to calculate; the formula is
Entropy(X) = - SIGMA log(P(x )) * P(x )
i i i
This does not depend on the values of X at all - only on how the probability is spread out across them. This quantity has a variety of interpretations and uses, but essentially it measures the smoothness of the distribution.
For example, suppose there are N different values for X with equal probability 1/N. Then the entropy is just -log(1/N) which is equal to log(N). For a flat distribution like this, the entropy thus increases with the number of possibilities. On the other hand, suppose the probabilities are all zero, except for a single value of X which always occurs - a maximally peaked distribution. For this, the entropy is zero (since log(1) = 0).
Entropy has a central role in information theory. If information about a variable's value is to be transmitted, then on average the amount of information needed to specify the value is given by the entropy of the distribution. If the logarithm is to base 2, entropy is measured in bits. If there are two equally likely possibilities for a variable, then both the formula and common sense indicate that 1 bit of information is needed to specify the variable's value.
Consider, for example, a linear neural network unit whose two inputs are random binary variables, which each independently take values -1 or +1 with equal probability. The variable X stands for the input vector, so its values are (-1,-1), (-1,+1), (+1,-1), (+1,+1), each with probability 1/4. The entropy of this distribution, using the formula above, is
- (1/4 * log(1/4) + 1/4 * log(1/4) + 1/4 * log(1/4) + 1/4 * log(1/4))
= - 4 * 1/4 * log(1/4)
= 2
because log(1/4) = -2 if we use logarithms to base 2. That is, X requires, not surprisingly, 2 bits of information to specify it.
Now suppose this unit simply sums its inputs. The output, Y, is a number whose values are -2, 0, 0, +2 respectively for the 4 possible inputs. There are only 3 values of Y, with probabilities P(-2) = 1/4, P(0) = 1/2, P(+2) = 1/4 (using the rule for combining probabilities for mutually exclusive events). Thus the entropy of Y is
- (1/4 * log(1/4) + 1/2 * log(1/2) + 1/4 * log(1/4))
= 1.5
That is the output Y has a lower entropy - it transmits less information - than the input X. The reason is, of course, that information has been lost in the addition, as the two cases when the inputs are different cannot be distinguished in the output.
The idea of 1.5 bits might seem strange. Remember, though, that this is a measure of the amount of data needed to specify Y on average, if the process is done a lot of times. The entropy measures how well a perfectly efficient coding scheme could do in compressing the information carried by the output of the network when it is used repeatedly.
Entropy can also be viewed as a measure of disorder. The more disordered a system is, the more information is needed to specify it exactly. If the cells of a cellular automaton are all likely to be in any state with equal probability, then to transmit the state of the whole system we will need to transmit the state of each cell. The disorder is high, and calculating the entropy will give a large number. If, however, one state is much more likely than the others, then we need only transmit the state of the cells that are in one of the lower-probability states. The order is higher, and the entropy will work out as a lower number. Minus the entropy is sometimes called the negentropy and used as a measure of order in a system.
It seems worthwhile to include a brief note about random numbers in the context of computer simulations. Such simulations rely very heavily on so-called random numbers, usually generated by calls to library procedures such as C's rand routine. In fact, such numbers are actually pseudo-random, since they are generated using a deterministic algorithm that produces a completely predictable sequence. True random numbers which are independent of one another form a completely unpredictable sequence.
Pseudo-random number algorithms are designed to be (a) fast and (b) produce numbers whose statistics are the same as far as possible as those of true random numbers. Thus the mean, standard deviation and so on of the numbers themselves, and higher-order statistics such as the mean of differences between successive pairs of numbers, will be within the expected ranges for uniformly distributed true random numbers.
Usually, there is no need to worry unduly about using these generators: their properties have been well worked out and they are adequate for most simulations. However, there have been one or two cases in which standard libraries have contained very poor generators, in that, for example, successive "random" values have been correlated with one another. It is worth bearing in mind this possibility: if a simulation is not behaving as expected, and all else fails, it might be worth trying using random numbers from a different routine.
In addition, for large, delicate simulations, there is a rule of thumb that suggests that the number of values extracted from a pseudo-random generator should not exceed the square root of the cycle length (or period) of the generator (the number of values it produces before repeating itself). A reputable generator will state its cycle length in its documentation - e.g. the implementation of rand on my machine has a period of 2^32, so should ideally not be used for more than 2^16 = 65,536 values in any one simulation. Fortunately much better generators are easily available.
Do not be tempted to try to improve the properties of a pseudo-random generator by resetting it from time using, say the system clock, memory usage or some other "random" value from outside the program. Such strategies will almost always degrade the statistical properties of the generator.
One question that often arises in practice is how to get pseudo-random numbers that have approximately a given distribution. Most pseudo-random generators provide numbers drawn from a uniform distribution with cumulative probability F(x) = x, with 0 <= x < 1. Suppose we need to simulate a random variable Y with cumulative probability distribution G(y). If X and Y are related by X = G(Y), then it is possible to show that Y has the required distribution. Thus to convert directly from values produced by the generator to the required values, it is necessary to compute the inverse of the required cumulative distribution function for each value generated. This can be difficult and computationally costly in some cases.
There is a very rough-and-ready short cut for approximate Gaussian distributions: adding 12 uniformly distributed random numbers in the range 0-1 together gives a value which is roughly from a Gaussian distribution with mu = 6 and sigma = 1. You can scale and shift this to approximate any Gaussian distribution, provided an accurate distribution is not needed. Using more than 12 inputs gives a better approximation; the mean will be half the number of values added and the standard deviation the square root of the number of values divided by the square root of 12.
Dealing with uncertainty is the central problem in prediction and control. Probability is the calculus of uncertainty, and statistics are the tools used to draw inferences from data within a probabilistic framework. The topics mentioned above - probability distributions and simple statistics - are the starting point for a great deal of sophisticated analysis. In particular, the theory of statistical inference is a large and complex one.
However, for many practical problems, a clear idea of what is meant by a probability distribution and by the mean and standard deviation (and possibly the entropy) can be put to good effect in straightforward ways.
Copyright University of Sussex 1997. All rights reserved.