|
| Discrete Dynamics Lab |
The spiral glider-gun rule, v=3 k=7
Further details and results relating to the paper:
Wuensche,A., A.Adamatzky, (2006),
"On spiral glider-guns in hexagonal
cellular automata: activator-inhibitor paradigm"
to appear in International Journal of Modern Physics C (preprint online
here)
| Fundamental structures in the spiral rule, which can be interpreted as a reaction-diffusion system (activator, inhibitor and substrate). Note also that the dynamics are symmetric — all phenomena can occur equally in any direction, or clockwise and anti-clockwise. | ||
 5 basic types of mobile gliders (G1-G5), all travelling NorthEast, in the direction of their "active" red heads. |
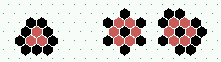 2 types of static "eaters" (E1, E2), E2 has "memory" on its outer shell | |
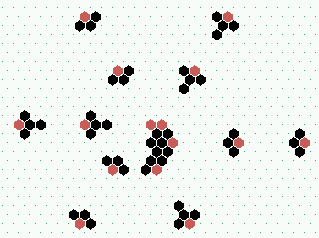 S1: high-frequency spiral glider-gun shooting G1 gliders, frequency=6 |
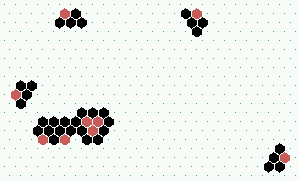 S2: low-frequency spiral glider-gun shooting G2 gliders, frequency=21 | |
| S1 and S2 spiral glider-guns, 120x120, click to enlarge | ||
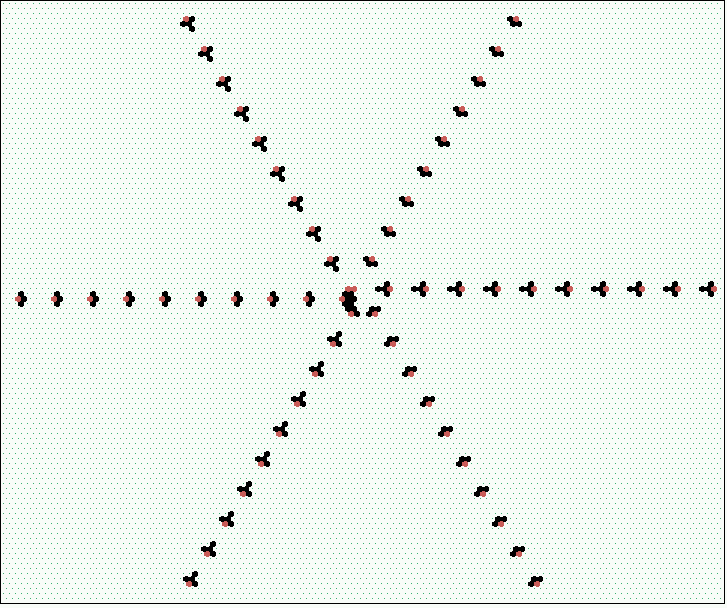 S1: high-frequency spiral glider-gun |
 S2 low-frequency spiral glider-gun |
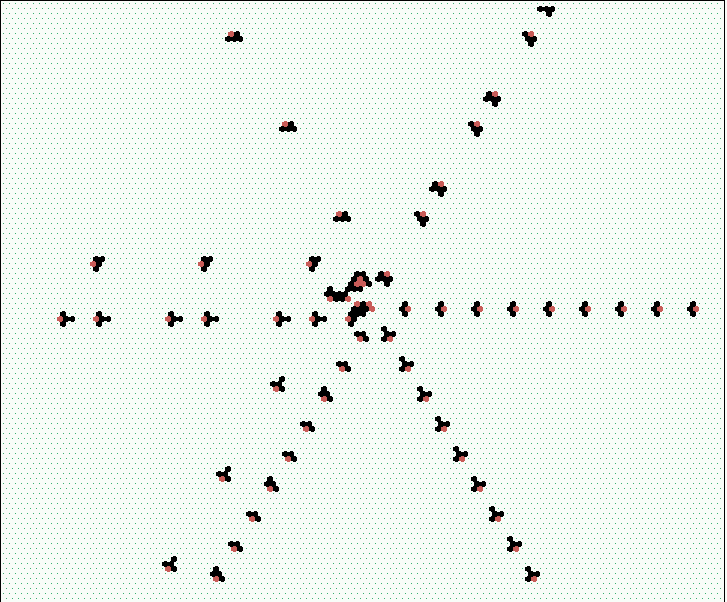 high and low-frequency spiral glider-guns interacting |
|
Polymer gliders and eaters forming chains, aggregations and oscillators of arbitrary length, can exist in many combinations. |
 Various types of small 2-headed gliders heading NE. |
 Examples of linked eaters. |
| Snapshots of evolved systems, with gliders, glider-guns and eaters, forming quasi-stable circuits, click to enlarge. | |
 snapshot 88x88 |
 snapshot 250x250 |
|
72 single mutations to the spiral rule 36 are quasi-neutral. Click to enlarge. The initial state is the 88x88 snapshot above. | ||||||||
| index 0-5 | 0
| 1
| 2
| 3
| 4
| 5
| ||
| index 6-11 | 6
| 7
| 8
| 9
| 10
| 11
| ||
| index 12-17 | 12
| 13
| 14
| 15
| 16
| 17
| ||
| index 18-23 | 18
| 19
| 20
| 21
| 22
| 23
| ||
| index 24-29 | 24
| 25
| 16
| 27
| 28
| 29
| ||
| index 30-35 | 30
| 31
| 32
| 33
| 34
| 35
| ||
| Pairwise collisions between basic gliders - some examples |
| Mutual annihilation 2→0 | |||||||
| 3 steps |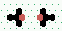 
| 
| 
| 3 steps |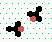 
| 
| 
|
| Conservation + Destruction 2→1 | |||||||
| 2 steps | 
| 
| 
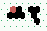
| 2 steps |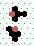 
| 
| 
|
| One glider bouncing off another 2→2 | |||||||
| 180° bounce 6 steps |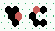 
| 
| 
| 
| 
| 
| 
|
| 120° bounce 7 steps | 
| 
| 
| 
| 
| 
| 
| 
|
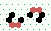
| Reproduction | |||||||
| 2→4 6 steps | 
| 
| 
| 
| 
| 
| 
|
| 2→6 10 steps |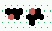 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
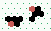
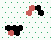
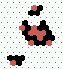
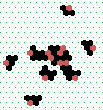
| 2→8 13 steps |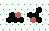 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
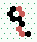
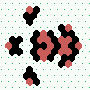
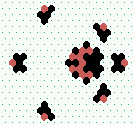
| 2→6 15 steps |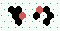 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
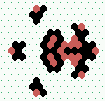
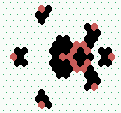
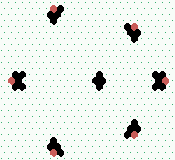
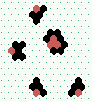
| Creating eater E1 | |||||||||||
| eater E1 + 4 gliders 10 steps | 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
| Memory - Glider interacting with eater E2 | ||||||
| Write | 
| 
| 
| 
| 
| 
|
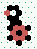
| Read | 
| 
| 
| 
| 
|
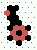
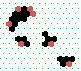
| Creating spiral-glider guns S1 and S2 |
S1 spiral glider-gun | 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| |||||||
|
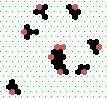
S1 spiral glider-gun | 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
|
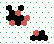
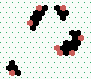
S2 spiral glider-gun | 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
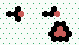
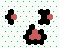
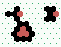
| mobile gliders-guns, some examples, with heading (moving head direction) indicated | |||
heading NE
| heading NE
| heading NE
| heading NE
|
heading NE
| heading East
|
Building the spiral rule
The lookup table
v=3 cell-states (cell-values) [2, 1, 0] are represented by cell-colors:
black, red, white in the examples above.
A cell updates its state depending on the totals of [2s, 1s, 0s] in its
neighborhood, size k=7 — the cell and
its nearest neighbors on a lattice
with hexagonal tiling. There are
S = (vk - 1)! / (k!(v -1)!)
possibilities,
so 36 [2, 1, 0] sub-rules (and their outputs) set out in DDLab's format
below. The output string
defines the rule (also represented in hexadecimal).
35 0 - rule-table index
| |
2:766555444433333222222111111100000000
1:010210321043210543210654321076543210
0:001012012301234012345012345601234567
||||||||||||||||||||||||||||||||||||
000200120021220221200222122022221210 = 020609a2982a68aa64 in hexadecimal
The filename of the spiral rule in DDLab is v3k7w1.vco
k7 hex neighbourhood
The consequences of mutating the spiral glider-gun rule's lookup table
Each lookup table output (subrule) has two possible mutations, 72 in all,
This table indicates the consequences of each mutation, and which subrules are
quasi-neutral (+,-), and which are responsible for gliders (>). This relates to the
neighborhood frequency histogram, the frequency of sub-rules in the evolving CA.
A snapshot of each mutation is shown below.
rule-table index
/ totals: 2s+1s+0s=k=7
/ / rule-table
/ / / mutations neighborhood frequency histogram
/ 2_1_0 / 2___1___0
0: 0 0 7 : 0 > o c . |||||||||||||||||||||||||||||| 85.7% =>
1: 0 1 6 : 1 > o . o |||||||||||| 0.7%
2: 0 2 5 : 2 . g g ||
3: 0 3 4 : 1 + G . G |
4: 0 4 3 : 2 - . G G :
5: 0 5 2 : 2 - . G G :
6: 0 6 1 : 2 + . G G :
7: 0 7 0 : 2 + . G G :
8: 1 0 6 : 0 > c c . |||||||||||||||||||||||||||||| 4.5% =>
9: 1 1 5 : 2 > . c c |||||||||||||||||||||||| 1.4%
10: 1 2 4 : 2 . g g ||||
11: 1 3 3 : 1 + G . G |
12: 1 4 2 : 2 + . G G :
13: 1 5 1 : 2 + . G G :
14: 1 6 0 : 2 + . G G ||
15: 2 0 5 : 0 > c c . |||||||||||||||||||||||||||||| 2.3% =>
16: 2 1 4 : 0 > o c . ||||||||||||||||||||||| 1.3%
17: 2 2 3 : 2 . c g ||||
18: 2 3 2 : 1 - G . G ||
19: 2 4 1 : 2 + . G G |
20: 2 5 0 : 2 + . G G ||
21: 3 0 4 : 0 > g c . ||||||||||||| 0.8%
22: 3 1 3 : 2 > . c g |||||||||||||||||||||||||| 1.6%
23: 3 2 2 : 2 . g g ||||||
24: 3 3 1 : 1 g . g ||||
25: 3 4 0 : 2 - . G G |
26: 4 0 3 : 0 g G . |||
27: 4 1 2 : 0 > G c . ||||||||||
28: 4 2 1 : 2 . cg g ||
29: 4 3 0 : 1 g . g ||||||||
30: 5 0 2 : 0 G c . ||
31: 5 1 1 : 0 > G c . |||
32: 5 2 0 : 2 - . G G ||
33: 6 0 1 : 0 G c . ||
34: 6 1 0 : 0 G cg . ||
35: 7 0 0 : 0 - G G . |
Key to mutations
G:quasi-neutral, g:related but different glider dynamics emerge
c:chaotic, cg:tends to chaos but with gliders present o:order.
36 mutations and 15 sub-rules are wildcards, making no impact, or minimal impact
on the dynamics. Sub-rules are marked as:
+strong wildcards (9), –weak wildcards (6),
and >glider-critical (10)
The rule as a matrix
The rule can be represented more simply as an ij matrix as shown below,
were i represents the number of 2s, and j the number of 1s.
The number of 0s follows: 7-(i+j). The output of each sub-rule
can be read off each ij. The matrix on the right shows: +:strong
wildcards, and –:weak wildcards.
the spiral glider-gun rule as a k=7 matrix
j=1s wildcards
0 1 2 3 4 5 6 7 -weak +strong
...............
0: 0 1 2 1 2 2 2 2 0 1 2 + - - + +
1: 0 2 2 1 2 2 2 0 2 2 + + + +
2: 0 0 2 1 2 2 0 0 2 - + +
i=2s 3: 0 2 2 1 2 0 2 2 1 -
4: 0 0 2 1 0 0 2 1
5: 0 0 2 0 0 -
6: 0 0 0 0
7: 0 -
neighbourhoods frequency histogram:
snaphot from DDLab
The rule as a k=6 outer-totalistic rule
The same rule can be expressed as a k=6 outer-totalistic rule,
which consists of three centre-rules, one for each state (or value [2, 1, 0])
of the central cell, c. Each centre-rule has 28 sub-rules, which are
shown in the DDLab format, and
tabular and matrix form below, indicating strong (+), and weak (-) wildcards.
28 0 - rule-table index
| |
| 2:6554443333222221111110000000
v| 1:0102103210432105432106543210
| 0:0010120123012340123450123456 hexadecimal filename in DDLab
|||||||||||||||||||||||||||| -------------- ----------
| 0:0002001220212002212202221210 - 020689829a2a64 w1otc0.vco
c| 1:0201202122221202221222222121 - 2189aa62a6aa99 w1otc1.vco
| 2:0002001200212202212002221220 - 020609a2982a68 w1otc2.vco
3 k=6 outer-totalistic rules
rule table index
/ totals: 2s+1s+0s=k=6 3 k=6 outer-totalistic matrices
/ / rule tables
/ / ---------------- j=1s wildcards
/ 2_1_0 C=2 C=1 C=0 0 1 2 3 4 5 6 -weak +strong
0: 0 0 6 : 0 1 0 .............
1: 0 1 5 : 2 2 1 c=2 0: 0 2 2 1 2 2 2 0 2 2 + - - +
2: 0 2 4 : 2 1+ 2 1: 0 0 2 1 2 2 0 0 2 - + +
3: 0 3 3 : 1+ 2- 1+ 2: 0 2 2 1 2 0 2 2 1 -
4: 0 4 2 : 2- 2- 2- i=2s 3: 0 0 2 1 0 0 2 1
5: 0 5 1 : 2- 2+ 2- 4: 0 0 2 0 0 -
6: 0 6 0 : 2+ 2+ 2+ 5: 0 0 0 0
7: 1 0 5 : 0 2 0 6: 0 0
8: 1 1 4 : 0 2 2
9: 1 2 3 : 2 1+ 2
10: 1 3 2 : 1- 2+ 1+
11: 1 4 1 : 2+ 2+ 2+ c=1 0: 1 2 1 2 2 2 2 1 2 + - - + +
12: 1 5 0 : 2+ 2+ 2+ 1: 2 2 1 2 2 2 2 2 + + + +
13: 2 0 4 : 0 0 0 2: 0 2 1 2 2 0 2 - + +
14: 2 1 3 : 2 2 0 i=2s 3: 2 2 1 2 2 2 1 -
15: 2 2 2 : 2 1- 2 4: 0 2 1 0 2 1
16: 2 3 1 : 1 2+ 1- 5: 0 2 0 -
17: 2 4 0 : 2- 2+ 2+ 6: 0 0
18: 3 0 3 : 0 2 0
19: 3 1 2 : 0 2 2
20: 3 2 1 : 2 1 2
21: 3 3 0 : 1 2- 1 c=0 0: 0 1 2 1 2 2 2 0 1 2 + - - +
22: 4 0 2 : 0 0 0 1: 0 2 2 1 2 2 0 2 2 + + +
23: 4 1 1 : 0 2 0 2: 0 0 2 1 2 0 0 2 - +
24: 4 2 0 : 2- 1 2 i=2s 3: 0 2 2 1 0 2 2 1
25: 5 0 1 : 0 0 0 4: 0 0 2 0 0 2
26: 5 1 0 : 0 2- 0 5: 0 0 0 0
27: 6 0 0 : 0- 0 0 6: 0 0
k6 outer-totalistic
hex neighbourhood