Introduction. In the lectures we saw how a finite state automaton (FSA) can be represented by a 2-dimensional matrix. In this task you should write a simple FSA that takes as input a matrix and then decides the language given by the matrix. Note that the specification below is wordy, but the task is very simple: my example solution is 11 lines of plain Java code, and it's not importing any libraries.

Task. You are asked to produce a Java program that takes as input a 2-dimensional matrix together with an initial and terminal state (representing an FSA). Your submission should return a Java algorithm instantiating the interface Language (given below) that correctly decides the language given by the input FSA.

Let's make this more precise. As characters we only allow integers. States are also integers. More precisely:

• Alphabet. We assume that the alphabet of any given language is always of the form {0, 1, ..., m} for some fixed integer m. (The m might be different for different languages.)
• States. We assume that the states of any given FSA is always of the form {0, 1, ..., n} for some fixed integer n. (The n might be different for different FSAs.)
• Terminal state. We assume exactly one terminal state, which must be one of {0, 1, ..., n}.

The signature that characterises the input that your submission needs to process is:

interface Matrix2D {
    public int initialState ();
    public int terminalState ();
    public int nextState ( int currentState, int character ); }
	  

You can think of nextState( s, c ) as giving the entry in the 2-dimensional matrix at row s and column c. Your solution to Task 1 must be of the following form:

class Task1 {
    public static Language create ( Matrix2D matrix2D ) { return ...; } }
	  

In other words, you must submit a working implementation of the class Task1. This means you must replace the ... by actual Java (and add other code). You can think of create as a 'language factory' that, when called, returns an instance of the interface Language. You will have to submit the Java for this instance. In other words, create takes as input a matrix (an instance of the Matrix2D interface) representing an FSA, and returns an object deciding the language given by the matrix. The Language interface is as follows:

interface Language {
    public Boolean decide ( int [] input ) throws Task1Exception; }
	  

The decide method takes as input a 'string', here represented for simplicity as an array of integers (recall the assumption above that the characters making up the alphabet are integers). The requirement is that decide returns true exactly when the input string is in the language of the input to the create method.

If the decide method that you provide encounters an error condition, use Task1Exception to report it. Do not throw any other exceptions. Note that you do not have to throw an exception if you don't want to.

class Task1Exception extends Exception {
    public String msg;
    public Task1Exception ( String _msg ) { msg = _msg; } }

You can find this code here.

You can assume that all instances of Matrix2D will only contain valid states as entries. In other words: whenever s is a valid state, and c is a valid character, then nextState( s, c ) will return a valid state.

Note that Matrix2D does not explicitly state which integers are states and which integers are characters. This is not necessary for your algorithm to work. You can assume that all tests that I will run against your code only use 'strings' (here of given by an array int []) that contain characters in the relevant alphabet. In other words, the instances of Matrix2D you will be given can handle any 'string' my tests use. There is no need to cater for out-of-alphabet characters.

Note also that you do not have to supply classes instantiating the Matrix2D interface.

Examples. Consider the alphabet {0, 1} and the language of all binary strings over this alphabet. The following instance of Matrix2D is one possible implementation deciding this language.

class BinaryNumbers implements Matrix2D {
    private int [] [] fsaTable = new int [] [] { { 0, 0 } };	
    public int initialState () { return 0; };
    public int terminalState () { return 0; };
    public int nextState ( int currentState, int character ) {
	return fsaTable [ currentState ] [ character ]; } }
	  

Clearly BinaryNumbers implements the FSA given by this picture (red numbers are states, black numbers represent characters from the alphabet).

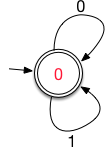
As a second example, again over the alphabet {0, 1}, consider the language of all binary strings divisible by 4. The following instance of Matrix2D is one possible implementation deciding this language.

class BinaryNumbersDivisibleBy4 implements Matrix2D {
    private int [] [] fsaTable
        = new int [] [] { { 0, 1 }, { 2, 1 }, { 0, 1 } };
    public int initialState () { return 0; };
    public int terminalState () { return 0; };
    public int nextState ( int currentState, int character ) {
	return fsaTable [ currentState ] [ character ]; } }
	  

Clearly BinaryNumbersDivisibleBy4 implements the FSA given by this picture (red numbers are states, black numbers represent characters from the alphabet).

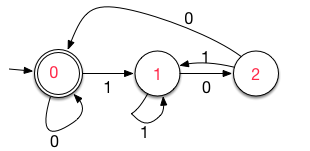
Note that your submission might be tested with input over larger alphabets of integers. You may also encounter automata where initial and terminal state are not identical.

The necessary Java files for all three tasks can be found for convenient download here:

• Zip archieve
• Github repo

Warning. Your code needs to compile against the signatures given to you here. Do not change them. You are welcome to add new classes. For your convenience you can find a file tester-skeleton1.java here that you can use to check if your submission compiles properly. Just download it, added to the directory containing all the files you want to submit, and run javac *.java. Note that tester-skeleton1.java does not test if you code has the right functionality. You will have to create and run your own tests to do that.