Maths Tools for Cognitive Scientists Lab 2 (Week 3)

Part b

http://www.informatics.sussex.ac.uk/users/bg22/mtcs/mtcs2b.html

1. Rules for differentiation: addition.  

   The derivative of the sum of two functions is simply the sum of the derivatives of each function:

   

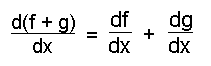
   (The rule also applies to subtraction.)

   For example if f(x) = x²  and g(x) = 3x then d(f+g)/dx = 2x + 3.

   Plot the following functions:
   

   • sin(x) + 4x²
   • 3x - cos(x)

   Now calculate their derivatives and plot the functions and their derivatives together.

    

2. Rules for differentiation: products.

   The derivative of the product of two functions is:

   

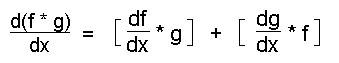
   For example if f(x) = x² and g(x) = sin(x) then d(f * g)/dx = [ 2x*sin(x) ] + [ cos(x)*x² ]

   What are the derivatives of the following products?
   

   • 5x * cos(x)
   • x³ * x² 

    

3. Rules for differentiation: the chain rule:

   If a function is applied to the result of another function (composite function) then the chain rule can be applied:

   

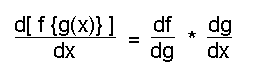
   For example if f(x) = (x² + 3)⁴ then f{g(x)} = g(x)⁴ (where g(x) = x² + 3)

   Therefore df/dg = 4(x² + 3)³ and dg/dx = 2x so d(f{g(x)})/dx = 4(x² + 3)³ * 2x.

   Plot the following curve between x values -2 and +2:

   • sin(5x)

Now calculate the derivative and plot its curve on the same figure.

 

 

4. Rules for differentiation: partial derivatives.

   If a function has more than one variable then partial derivatives are found for each variable
   while the other variables are held constant. 

   For example given a function of x and y :

   f(x,y) = x² sin(y) 

   The partial derivative of the function with respect to x (considering y to be a constant value) is:

   

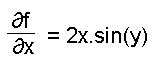
   And the partial derivative with respect to y (consider x to be of constant value):

   

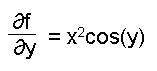
   Find the partial derivatives of x, y and z in the following function:

   • x³ + 5y² -sin(z)

 

5. Optional: derivative of the logistic sigmoid

   The logisitc sigmoid function shown below has a very simple derivative if
   defined in terms of itself.

   

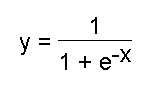
   Find the derivative dy/dx of this function and express your answer
   in terms of y.

   Some helpful hints:

   • The derivative of e^ax is ae^ax.
   • The equation can be expressed as y = ( 1 + e^-x)^-1.
   • (u - 1) / u can also be expressed as 1 - (1/u)