Research Methods 1: Statistics Problem Sheet 1: (Means, S.D.'s and the Normal Distribution):

[These problems can be answered once you have covered the material on means, standard deviations and z-scores].

1. Here are twenty scores on a statistics aptitude test:

15, 7, 23, 19, 4, 10, 13, 17, 2, 30, 14, 17, 22, 15, 12, 18, 4, 18, 13, 21.

(a) Calculate the mean and median for these scores. [Answers: 14.7, 15.0].

(b) Calculate the standard deviation of these two scores, in two ways:

(i) as a description of this particular sample; [answer: 6.83].

(ii) using this sample in order to estimate the standard deviation of the population of scores from which it is presumed to have been taken. [Answer: 7.00].

(c) If the scores were normally distributed, what proportion of the scores would you EXPECT to be within one standard deviation of the mean? [Answer: 68%].

(d) What proportion of scores are ACTUALLY within one standard deviation of the mean (taking the s.d. as being 7.00)? [Answer: 65%].

2. An experimenter times how long it takes normal adults to fall asleep during a Disney film. Here are the times for sixteen adults (measured in seconds):

400, 450, 504, 534, 486, 600, 615, 490, 558, 449, 998, 500, 408, 590, 586, 998.

(a) Draw a graph of the grouped frequency distribution of times, using a class interval width of 50 (starting at 351) .

(b) Calculate the mean, median, mode and s.d. (using the n-1 formula for the s.d.) of the scores. [Answers: mean = 572.9, s.d. = 178.5, median = 519.0, mode = 998].

(c) Redo (b), but omitting the two scores of 998. What do you notice? [Answers: mean = 512.1, s.d. = 70.7, median = 502.0, mode = incalculable].

3. On a standard test of reading ability, a group of 173 normal patients have a mean score of 86, with a standard deviation of 6.5. Following a head injury, patient X now scores 75 on the same test.

(a) Convert 75 into a z-score. What would you conclude about patient X's performance, relative to the normal patients? [Answer: -1.69].

(b) What proportion of the normal patients would be expected to score 75 or less? [Answer: 0.0455].

(c) What proportion of the normal patients would be expected to score 86 or more? [Answer: .50]

(d) What proportion of the normal population would be expected to score between 84 and 92? [Answer: 0.4429].

(e) How MANY patients would be expected to score between 84 and 92? [Answer: 77 patients].

(f) How MANY patients would be expected to score higher than patient X, i.e. 75 or more? [Answer: 165 patients].

Research Methods 1: Worked Solutions to Statistics Problem Sheet 1: (Means, S.D.'s and the Normal Distribution):

QUESTION 1:

Part (a)

To calculate the mean, add together all of the scores and divide by the number of scores: 294/20 = 14.7. To calculate the mean, arrange the scores in numerical order. If there is an odd number of scores, the median is the middle score - i.e., the score for which there are as many scores above it as below it. If there is an even number of scores, the median is the average of the middle two scores. In this case, the two middle scores are 15 and 15, so the median is (15 + 15)/2 = 15.

Part (b)

The standard deviation is a measure of the variability of our data: the bigger the s.d., the more the scores are spread out. The s.d. can be used in two ways. It can be used purely as a description of the sample from which it is obtained. However, we often wish to go beyond this: we hope to make extrapolations from our handful of subjects to the whole of humanity. It is almost never possible to work out the actual mean and s.d. of our population, and so we have to make do with estimates of these population measurements; these estimates are made on the basis of our sample.

The mean of a sample is a good estimate of the mean of the population from which the sample is derived, and so we can use the same formula in both cases. However, this is not the case when it comes to standard deviations: it can be shown that the sample standard deviation tends to underestimate the size of the true population standard deviation if it is used as an estimate of the latter. Therefore, we need to add a small "correction" to the sample s.d. formula in order to make it a better estimate of the population s.d. This correction consists of dividing by the number of scores minus one, rather than dividing by the number of scores. The effect of this bodge is to make the s.d. larger than it would otherwise have been. This is why the sample s.d. (using the "n" formula) is 6.87, but the estimated population s.d. (using the "n-1" formula) is 7.00.

To calculate the sample s.d. by hand:

(i) calculate the mean of the scores (14.7);

(ii) subtract the mean from each of the scores, to get a set of 20 "remainders";

(iii) square each of these remainders, to get rid of the minus signs;

(iv) add up these numbers to get a grand total;

(v) divide the total obtained in (iv) by either the number of scores or the number of scores minus one (depending on whether you want the sample s.d. or want to use the sample s.d. as an estimate of the population s.d.);

(vi) you now have the variance; take the square root of this to get the standard deviation.

In detail....

step (ii) step (iii) step (iv) step (v) step (vi)

0.3 0.09 932.20 46.61 (using n=20) 6.83

-7.7 59.29 49.06 (using n-1) 7.00

8.3 68.89

4.3 18.49

-10.7 114.49

-4.7 22.09

-1.7 2.89

2.3 5.29

-12.7 161.29

15.3 234.09

-0.7 0.49

2.3 5.29

7.3 53.29

0.3 0.09

-2.7 7.29

3.3 10.89

-10.7 114.49

3.3 10.89

-1.7 2.89

6.3 39.69

In practice, this would be a very laborious way of calculating an s.d.: either use one of the "computational" short-cut methods described in most textbooks, Excel, SPSS, or the standard deviation function on your calculator!

Part (c)

You should know that 68% of scores in a normal distribution fall within one standard deviation either side of the mean; 95% fall within two s.d.'s; and 99.7% fall within three s.d.'s. This is a theoretical expectation however: in practice, the values obtained will usually be slightly different. To work out what proportion of our scores actually fell within one s.d, of the mean is quite easy. Our mean is 14.7, and our s.d. is 7. We want to know how many scores fell within the range of 14.7 + 7 and 14.7 - 7: i.e., how many scores were between 7.7. and 21.7.

13 of our 20 scores fell within these limits. To express this as a percentage: (13/20)*100 = 65%. This actual figure compares quite favourably with the expected figure of 68%.

QUESTION 2.

Part (a)

Your grouped frequency distribution should have looked like this:

score: frequency: score: frequency: score: frequency:

351-400: 1

401-450: 3 601-650: 1 801-850: 0

451-500: 3 651-700: 0 851-900: 0

501-550: 2 701-750: 0 901-950: 0

551-600: 4 751-800: 0 951-1000: 2

Part (b)

To calculate the mean, add up all the scores and divide by the total number of scores:

9166/16 = 572.89.

To calculate the standard deviation (using the n-1) formula:

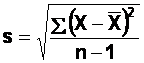
In English, this means:

(i) subtract the mean of the scores (572.89) from every score, to get a set of difference scores;

(ii) square each of the difference scores thus obtained;

(iii) add together all of these squared difference scores;

(iv) divide the result of (iii) by the number of scores minus one (i.e., 15 in this case), to get what's called the variance;

(v) take the square root of the result of (iv), to get the standard deviation. The answer you should have is 178.5.

To calculate the median, arrange all the scores in order of size and take the middle score (if there is an odd number of scores), or the average of the middle two scores (if there is an even number of scores). Here, we have an even number of scores, so we do the latter:

400, 408, 449, 450, 486, 490, 500, 504, 534, 558, 586, 590, 600, 615, 998, 998.

The median is (504+534)/2 = 519.

The mode is the most popular score: here the only score which occurs more than once is 998, so that's the mode.

Take note of a couple of points about these statistics. Firstly, the mean, median and mode are quite different from each other. This suggests that the data are skewed - that is, they are not symmetrically distributed around the mean. Looking at the frequency distribution shows that this is clearly the case: in this example, low scores predominate, except for the two odd high scores. (We might question why these two high scores have arisen, since they are so different from the rest of the data. Was it because the experimenter timing the subjects also fell asleep during the Disney film? Or do these two high scores come from individuals who were different in some important way from the rest of the subjects, for example in being aesthetically challenged individuals not representative of the normal population?) The two high scores have distorted the mean, median and mode to different extents: they have biased the mean upwards, and the mode is totally unrepresentative of the bulk of the data. One virtue of the median is that it is relatively unaffected by extreme scores.

(c) Recalculating the statistics with the two scores of 998 omitted produces a mean of 512.1, a s.d. of 70.7, and a median of 502.0. Things you should have noticed are:

(i) There is now no mode, since each score occurs equally frequently.

(ii) The mean is now smaller, since the distorting effects of the two 998 scores has been removed. This is reflected in the s.d., which is now much smaller than it was.

(iii) The median is now the average of the middle two scores: (500 + 504)/2 = 502. Removing the two extreme high scores has affected the median much less than it affected the other statistics.

(iv) The mean and median are still different from each other, but there is less skew than before.

QUESTION 3.

Part (a)

The formula for converting a raw score into a z-score is:

Here, X is 75, is 86, and s is 6.5. So,

Thus the z-score corresponding to 75 is -1.692. Patient X is over one and a half standard deviations below the performance of the "average" patient. He is quite below average in reading ability.

Part (b)

It always helps to draw a rough graph of these kinds of problems, so that you can keep track of what it is you are trying to do:

?

X=75 X=86 s = 6.5

We need to know the area under the normal curve which lies beyond the z-score corresponding to patient X's raw score of 75. This area corresponds to the proportion of patients who could be expected to score 75 or less.

We already have the z-score, from part (a) above; all we need to do is consult a table of z-scores and areas under the normal curve, and look in the column which gives the "area beyond z". Our z-score is -1.692; since the normal curve is symmetrical, the area beyond a z-score of -1.692 is the same as the area beyond a z-score of 1.692: 0.0455. Thus the proportion of patients who would be expected to have scored 75 or less is 0.0455. To express this as a percentage, simply multiply the proportion by 100: 4.55% of patients would be expected to score 75 or less.

Part (c)

This one is easy, and can be worked out without doing any calculations! Since the normal distribution is symmetrical around its mean, 50% of scores would be expected to fall above the mean and 50% below it. 86 just happens to be the same as the mean of the distribution of patient's scores, so 50% (.50, expressed as a proportion) of patients would be expected to score 86 or above.

? = 0.5

86

Part (d)

This one needs to be done in a number of stages. As before, graphing the problem makes it more obvious what it is we are trying to do:

?

84 86 92

(i) Find the z-score for 84, and then use the "area between the mean and z" column to find the area under the normal curve between 84 and 86.

(ii) Find the z-score for 92, and then use the "area between the mean and z" column to find the area under the normal curve between 86 and 92.

(iii) Add together the two areas you have just found: this represents the area between the two extremes of 84 and 92, which in turn corresponds to the proportion of scores falling between 84 and 92.

The combined area is .4429; in other words, about 44.29% of patients would be expected to score between 84 and 92 on the reading test.

Part (e)

To get the number of patients obtaining scores between 84 and 92, multiply the proportion doing so by the total number of subjects. Thus, in this case, .4429 * 173 = 76.6 ; in other words, approximately 77 patients scored between 84 and 92.

Part (f)

We already know the area beyond the z-score corresponding to a raw score of 75. In this context, "area beyond" means "area below". Since the total area under the normal curve is 1, the area above 75 must correspond to the total area (1) minus the area below 75 (0.0455). Thus the proportion of subjects scoring 75 or above must be 1-0.0455 = 0.9545. Over 95% of the normal patients scored higher than patient X.

?

= 1, minus this:

75 86 75