THE UNIVERSITY OF SUSSEX

BA and BSc First Year Examination 2005

RESEARCH METHODS IN PSYCHOLOGY I

Example Exam

Time allowed 2 hours

Answer all questions

Write your answers ON THIS QUESTION PAPER

There are five sections to this paper: 1, 2, 3, 4, and 5. Each section carries 20% of the marks. You are advised to spend an equal amount of time on each section.

SECTION 1: BASIC CONCEPTS

In this section, a concept is given together with five alternative definitions, only one of which is correct. Indicate which of the definitions is correct by writing the appropriate letter in the table provided at the end of this section (2 marks per question):

1. The arithmetic mean is:

(a). a summary of some data estimated by adding all the numbers, and dividing by the number of numbers minus one.

(b) a summary of the data that is a measure of the population rather than the sample.

(d) a summary of the data in terms of the most common value of the data.

(e) none of the above.

2. If data from an experiment show "homogeneity of variance", it means that

(a) they must be analysed using a t-test.

(b) scores in each group or condition show comparable amounts of variance.

(d) they have been measured on an interval or ratio scale.

(e) none of the above.

3. The variance is always:

(a) a measure of how noisy the data are, relative to a control.

(b) the square of the standard deviation.

(d) a measure that changes if you add a constant to all of the data.

(e) none of the above.

4. The Null hypothesis is always:

(a) the hypothesis you believe before the experiment.

(b) the hypothesis you do not believe before an experiment.

(d) shown to be highly unlikely by a significant result.

(e) none of the above.

5. A Sample:

(a) is the test you perform.

(b) has a smaller or equal number of data points than the population.

(d) is the technical term for an individual data point.

(e) is the median of the standard deviation.

6. A type two error:

(a) is when one rejects the Null hypothesis when it is in fact true.

(b) is when one accepts the Null hypothesis when it is false.

(d) is the error of using the wrong test.

(e) is the error of using the same data twice.

7. A significant negative correlation between data sets always implies:

(a) that there is no relationship between the two sets of data.

(b) that the relationship between two sets of data is not a simple linear one.

(d) that the data consist mainly of negative numbers.

(e) none of the above.

8. A sample being unrepresentative always implies:

(a) that not enough data were collected.

(b) that the data are not normally distributed.

(d) that you cannot use this sample to make inferences about the population.

(e) none of the above.

9. If data are normally distributed, it implies:

(a) that the data are typical of the population.

(b) that the data consist of 1/0 or yes/no type data.

(d) that the data are always positive.

(e) that the data are based on ranks.

10. Independence always implies:

(a) that an experiment was conducted double blind.

(b) that a one tailed statistical test is appropriate.

(d) that the variance of two measurements does not differ significantly.

(e) that the mean of two measurements does not differ significantly.

Table for answers to section 1:

Section 1	Answer
Q1	e
Q2	b
Q3	b
Q4	d
Q5	b
Q6	b
Q7	c
Q8	d
Q9	c
Q10	c

SECTION 2: PERFORM THE TEST

A psychologist is interested in how "sadotoothpullerophobia" (fear of dentists) develops. On the basis of an initial questionnaire, two groups of adults are identified: a group who report having had bad experiences of dentists in their childhood, and a group who report no such experiences. For each participant, the length of time since they last went to the dentist (in months) is recorded. Given the data below, perform an appropriate test to determine whether bad experiences of dentists in childhood leads to an avoidance of dentists in adulthood. Show your calculations, and then report the final result in a form appropriate for inclusion in a lab report. (NB: be very careful that you have chosen the correct test for these data, because if you choose an inappropriate test you will receive no marks for this section, even if the calculations are correct)

Bad childhood experiences	OK childhood experiences
36	32
78	89
116	12
57	4
88	127
78	45
34	7

Table 1: the time (in months) since each participant last went to the dentist.

1. The data are meaurements of time, and hence ratio data. Mean and s.d. for the "bad" group are 69.57 and 29.40. For the "OK" group, the mean and s.d. are 45.14 and 46.62. With such small samples, it's hard to say whether the data are normally distributed. However, the data do appear to lack homogeneity of variance. You can tell this by looking at the s.d. in relation to the mean. For the "bad" group, the s.d. is only half the size of the mean, whereas for the "OK" group, the s.d. is proportionately much bigger - it's the same size as the mean, in fact. Therefore the spread of scores is much greater for the "OK" group than it is for the "bad" group. Therefore we'll do a Mann-Whitney test.

2. Results of the Mann-Whitney test:

(I used SPSS rather than working it out by hand, but you should include your calculations here).

Mean rank for "bad" group = 8.86. Mean rank for "OK" group = 6.14.

A one-tailed test is appropriate here, because we are making a specific prediction - that bad experiences of dentists in childhood will lead an avoidance of dentists in adulthood. (In other words, on average we would expect the group with bad childhood experiences to have visited a dentist a longer time ago than the group who had had OK childhood experiences).

Mann-Whitney U = 15 (N1 = 7, N2 = 7). This is not significant at the p = .05 level of significance.

3. Final write-up:

"For the group whose childhood experiences of dentists had been bad, the mean length of time since their last visit to the dentist was 69.57 months (s.d. = 29.40). For the group which had OK childhood experiences, the mean length of time was 45.14 months (s.d. = 46.62). A Mann-Whitney test showed that the two groups did not differ significantly in terms of the length of time since they last visited the dentist (U (N1 = 7, N2 = 7) = 15, p>.05, one-tailed test)".

SECTION 3: WHICH TEST?

In this section you will be given a brief description of an experiment and some data; you have to choose the appropriate test. Always give the most powerful test appropriate to the data. There are 10 questions, each worth 2 marks. For each question write the letter corresponding to the correct test in the table at the end of this section. (Do not write the name of the test itself in the table: if you do so, it will not be counted as an answer).

A. Wilcoxon.	F. Independent-means t-test.
B. Friedman.	G. Spearman's rho.
C. Mann-Whitney..	H. Pearson's r.
D. Kruskal-Wallis	I. Chi-Square.
E. Matched t-test.	J. One-way ANOVA.

1.. The heights of 600 children raised on a meat diet were recorded, together with the height of 700 children raised on a vegetarian diet. What test is required to test the hypothesis that meat eating increases height?

2. A study was performed to examine the effects of allergies on cognitive performance. One group of participants were allergy-free; another group suffered from severe hayfever; a third group suffered from eczema; and a fourth group had gluten intolerance. Each participant was given a battery of cognitive tests that resulted in a single score (out of 100). Which statistical test should the researchers use to see if allergies affect cognitive performance?

3. A study was performed to investigate the effects of alcohol on people's mood. Three groups of subjects were compared. One group had water; one group had 1 pint of beer; and the third group had one pint of vodka. Each subject's mood was assessed by a questionnaire that yielded a score out of 50. Which statistical test should the researchers use to test if alcohol affects mood?

4. A researcher is interested in comparing the effectiveness of four different scuba diving courses. He assembles a boat-full of divers (twenty from each course), and takes them to a nearby barrier reef. Each diver makes one dive, in which he attempts to stay safely below the water for 40 minutes. The researchers then measure the number of divers from each course who successfully return to the surface. Which test should the researcher use in order to see if there is a significant difference between the effectiveness of the different training courses?

5. School governors in the town of Hemmington are concerned that 2004 has been a particularly bad year for the exam results. Before resorting to new teaching methods, they consult a statistician. He is told the mean exam result for the past twenty years, plus the standard deviation of the results over that time. Which statistical test should he use in order to see if 2004's mean exam result was exceptionally bad?

6. Researchers wants to find out if there is a relationship between length of service in academia and levels of obsession. The obsession level of each of fifty lecturers was measured by questionnaire. The length of time that each lecturer had been in the university was also recorded. After collecting these data, it was found that the scores were somewhat skewed towards the "highly obsessive" end of the scale. Which test should be used to measure the strength of the relationship between obsession and length of time in employment?

7. Anecdotal evidence suggests that many comedians' choice of career can be traced to their childhood experiences of using comedy in order to avoid being bullied at school. 200 comedians and 300 member of the public were interviewed and asked whether or not this use of comedy was true of them personally. What test should be used to test the hypothesis that bullying encourages children to follow a career in comedy?

8. Ten children are each given four different toys to play with, and are asked to rate each toy in terms of how much they liked it. Which test would you use to assess whether the four toys are liked equally?

9. Three hundred bird watchers are given the choice between a telescope and a pair of cheap binoculars. 182 prefer the telescope. Which test would you use to determine whether or not this is a statistically significant difference in preference?

10. 200 drivers' performance was rated by a professional driving instructor under two conditions: while they drove for 30 minutes without distraction, and while they drove for 30 minutes using a hands-free mobile phone. What test would you use to determine whether mobile phone-use impaired driving performance?

Section 3	Answer
Q1	F
Q2	J
Q3	D
Q4	I
Q5	z-score ( left it out of the list of tests!
Q6	G
Q7	I
Q8	B
Q9	I
Q10	A

SECTION 4: WHAT ARE THE DATA?

In the following questions you are given some data, and the results of an over-enthusiastic research assistant, who, knowing nothing about statistics, has performed as many tests as they can think of (only one of which is appropriate). You are then presented with a number of questions. Decide which of the research assistant'sanalyses is correct, give the answer to the questions, and present the relevant statistics. You will get marks for choosing the correct statistics, presenting the data in an appropriate way, and coming to correct conclusions.

1. An experimenter develops a method that is proposed to help the memory of people with brain damage. The proposal is that these people have problems because when they make a mistake in recall, they cannot remember whether the mistake or the real answer was correct. Therefore they are given strong clues to the answer, to stop them ever making mistakes and hopefully improving their memory (this method is known as errorless learning). To test this method, the experimenter asked five victims of stroke and five head injury patients to learn the names of 20 of their carers. Ten of the names were learnt using errorless learning, and ten using simple trial and error. The data, which cannot be assumed to be normally distributed, follow:

Patient	Cause of injury	No of names learnt using trial and error	No of names learnt using errorless learning
A	stroke	7	4
B	stroke	7	7
C	stroke	6	6
D	stroke	6	6
E	stroke	5	3
F	Head injury	6	3
G	Head injury	3	4
H	Head injury	7	3
I	Head injury	5	4
J	Head injury	6	5

The researcher was not sure if what the difference between parametric and non-parametric was, or whether a correlation was appropriate, so all of these tests were performed:

Matched t-test t= 2.512 d.f. = 9 P < 0.035
Independent t test t = 2.177; d.f. = 18 p < 0.043
Mann Whitney U = 25 P = 0.053
Wilcoxon Z = -2.047 p = 0.041
Pearson product moment correlation = 0.252 p = 0.482
Spearman rho = 0.209 P = 0.562

(a) Does errorless learning work?(four marks):

No. The mean for the "trial and error" condition was 5.80 (s.d. = 1.23). The mean for the "errorless" condition was 4.50 (s.d. = 1.43). Since the data do not satisfy the requirements for a non-parametric tes (since they are apparently not normally distributed), a Wilcoxon matched-pairs test was performed. This revealed a significant difference between the two conditions (Z = -2.05, p<0.05, two-tailed test), but in the opposite direction to that which was expected - i.e., the patients learnt more names using trial and error method than they did using the errorless learning method. It could be argued that, given the hypothesis, we should have used a one-tailed test anyway. However, whichever test we used, our conclusion would be that errorless learning does not significantly improve parients' ability to learn names. (NB: Wilcoxon's test is reported as "Z" here, because I did the original analysis using SPSS, and SPSS converts W into a z-score).

(b). It is found that the data were entered incorrectly and though the results for trial and error and errorless methods are typed in the correct columns, it is not known whether the two results in each row correspond to the same subject. Does errorless learning work? Give the relevant statistics (four marks):

We would now have to use a Mann-Whitney test, since we have to treat the data as if they come from two different sets of participants. The answer is still "no", errorless learning does not work. There is no significant differencein name learning between the two groups (U (N1 = 10, N2 = 10) = 25, p= 0.053, two-tailed test).

(c). In an attempt to make up for this mistake, the research assistant looked at the results from a number of previous studies and claimed that it is reasonable to assume that the data are normally distributed (though it is still not known if the rows correspond to the same subject). Assuming normally distributed data, does errorless learning work? Give the relevant statistics (four marks):

The appropriate test to use now would be the independent means t-test. The answer is still "no". The "trial and error" group performed significantly better than the "errorless learning" group ( t(18) = 2.18, p < 0.05) on the name learning task.

2. An experimenter is interested in weather big wave surfers (people who regularly try and surf waves bigger than 10 feet) are highly impulsive. She therefore questioned 200 surfers who purchased a surfboard at “Surf City” and measured i) whether they surfed big waves more than once a month, and ii) measured their impulsivity using an impulsivity questionnaire which rates people as impulsive or not.

	Impulsive	Not impulsive	Total
Big wave surfer	75	25	100
Not Big wave surfer	65	35	100
	140	60	200

Chi squared test gave c2 = 2.38, d.f. = 1 P > 0.05
Pearson’s product moment correlation between surfing (1 does big wave, 0 does not) and impulsivity gave r2 = 0.151, N = 200; d.f. = 198 P < 0.05
Z test: mean number = 50; standard deviation of number = 23.8, z = (75-50)/23.8 = 1.05; P > 0.05

Are big wave surfers more impulsive? Give the relevant statistics in a form appropriate for inclusion in a results section (four marks):

All we have is the number of surfers falling into each permutation of surfing behaviour and impulsivity, so Chi-Square is the appropriate test to use. There is no significant association between surfing behaviour and impulsivity (c2 (1) = 2.38, p > 0.05). In other words, big wave surfers are no more impulsive than non-big wave surfers.

3. A researcher is interested in how if a particular drug affects appetite in rats. Twelve rats were tested twice; either with the drug or without the drug, in a random order. In order to feed, the rats need to climb a slope to get a food pellet, and the number of time the animal climbed the slope in a 5-minute period was recorded. There is no reason to believe that the number of pellets is normally distributed: The data follow:

Rat number	With drug	Without drug
1	2	1
2	5	4
3	4	3
4	6	5
5	2	1
6	6	5
7	4	2
8	4	6
9	6	5
10	6	3
11	7	6
12	3	3

Matched sample t-test t = 2.727 d.f. = 11 two tailed p = 0.02
Independent t test t = 1.3 d.f. = 22 two tailed p > 0.207
Mann Whitney U = 50.5 p = 0.207
Wilcoxon Z = -2.183 two tailed p = 0.029

Does the drug affect appetite? Give the relevant statistics in a form appropriate for inclusion in a lab report (four marks):

A Wilcoxon test revealed that the drug significantly affected the rats' appetitites (Wilcoxon Z = -2.18, p<.05 two-tailed test). With the drug, the rats climbed the slope a mean 4.53 times (s.d. = 1.68). Without the drug, they climbed the slope a mean 3.67 times (s.d. = 1.78).

SECTION 5: "DO WE BELIEVE THE HYPOTHESIS?" AND PRESENTING THE RESULTS

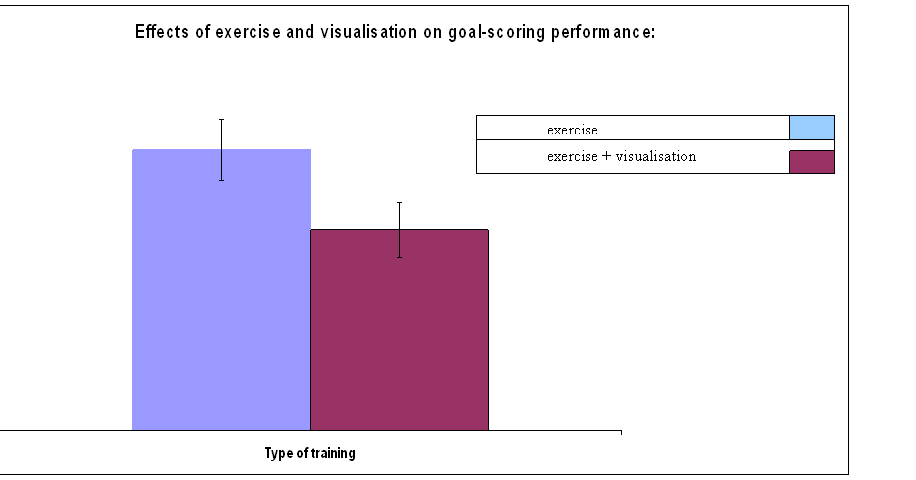
1. It is hypothesised that visualisation techniques combined with football training improve footballers' performance more than football training alone. This was assessed by measuring the number of goals scored in a season of training matches , after participants had either (a) trained for 5 hours a week on a running track and 5 hours a week in the gym; or (b) done this training plus five hours a week of visualising themselves scoring goals. The table below shows the number of goals that were scored by each player in the following season , together with the means, standard deviations, and t statistic for the unmatched t test used to compare the scores.

Subject number	Exercise alone	Exercise plus visualisation
1	5	9
2	14	7
3	13	6
4	17	15
5	12	5
6	11	6
7	19	12
8	11	13
Mean	12.75	9.125
Standard deviation	3.96074488	3.515590278

t = 1.81098

(a) Sketch a graph, together with standard error bars to summarise the data (4 marks).

(b) Describe the data in a form appropriate for inclusion in the results section of a paper (assuming no graph in the results section). (4 marks):

An independent means t-test revealed that the mean number of goals scored in a season of training matches was not affected by the training method used (t (14) = 1.81, p> .05). Players training by using exercise alone scored a mean 12.75 goals in the season (s.d = 3.96). Players using visualisation techniques combined with exercise scored a mean 9.13 goals in a a season (s.d. = 3.52).

(c) Based on these data, what can we conclude? (2 marks)

Visualisation plus exercise is no better as a training method than exercise by itself.

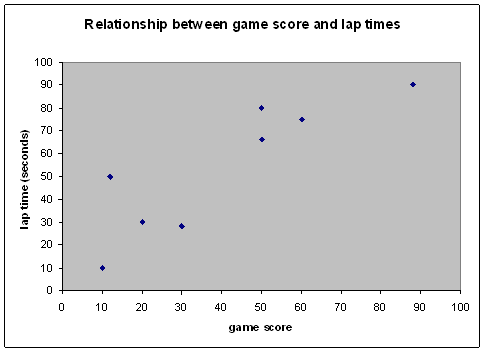
2. A paper starts with the hypothesis that the ability to perform well on a computer driving game is a good measure of a person's ability to drive fast on a real driving track. The table below shows eight subjects’ high scores in a racing game (a higher score meaning that they performed better), and their average lap time at Grands Patch racetrack. Also shown is the value of the correlation coefficient r calculated by computer.

Subject	Racing games score	Racing track lap time
number		(seconds)
1	20	30
2	50	66
3	30	28
4	60	75
5	88	90
6	10	10
7	12	50
8	50	80

r = 0.86819599

(a) Present the data graphically in a form appropriate for inclusion in a scientific paper. (4 marks).

(b) Describe the data in a form appropriate for inclusion in the results section of a paper (assuming no graph in the results section) (4 marks)

There was a significant relationship between participant's performance on the racing game, and their performance on the race track. The better their high score on the racing game, the slower their lap times at Grand Patch race track (Pearson's r = 0.87, p = 0.005). (Note: the correlation is a positive one, but because longer lap times are a reflection of poorer driving performance, what we really have is a negative relationship between game performance and driving ability: the better the gane performance, the slower the driver).

There is a strong relationship between driving game performance and people's ability to drive fast on a real racing track: the better the game performance, the slower people drive in real life.