This teach file complements FCS4. It provides two examples of the application of ideas in vector analysis.
The most immediate and obvious application of vectors is the representation of geometrical relationships in ordinary 3-dimensional space. This is not surprising, since the prototype vector is a position vector. This file concentrates on this kind of use for vectors, but it is worth bearing in mind that much more abstract entities also lend themselves to vector representation, as we have already seen in the case of input and weight vectors for neural networks.
The need to represent geometrical relationships arises particularly often in those parts of robotic or a-life systems which have to interact with the physical world (or a simulation of it). Perceptual and motor control systems frequently use vector representations of space (and sometimes of space-time).
Here, I focus on matrix-vector multiplication, since this linear operation is one of the most important in applied mathematics.
The common functions, such as sin and log, take a number as argument and produce (or "map onto") another number. There is nothing to stop us extending the idea of a function to include vector functions, which take one or more vectors (and maybe numbers as well) as arguments and which produce vectors as their result.
If the input to such a function is a position vector, and the result is another vector, then we have a vector field. For example, if the wind speed and direction at each point at ground level in Sussex is represented by a vector, the set of vectors forms a 2-D vector field. Graphically, the wind over Sussex might be displayed as arrows drawn on a map, and this provides a way to visualise the vector field idea.
The wind velocity vector at a point has two components (one might represent it using northerly and easterly components for example). It's not absolutely obvious that velocities should be manipulated in the same sort of way as positions, but in fact it's the case that the same vector rules are appropriate for velocities, and the rules have straightforward physical meanings (at least as long as the speeds are small compared to that of light). In other words, if positions are appropriately represented by vectors, then so are velocities.
If the wind velocity was represented by a vector v, and position on the ground by a vector r, then we could write
v = f(r)
where f is the name of the vector function that assigns a wind velocity to each point on the ground. Of course in this example the function would not be a simple thing to write down - the best you could probably do would be to tabulate an approximation to it - but the idea that you can associate a velocity vector with each position vector in the domain of the function (here Sussex) is what matters. Often the shorthand notation v(r) is used to indicate that v depends on r, without giving the function a separate name.
If the vertical component of the wind velocity was represented as well, and the position included height above the ground, then we would have a function from 3-D position vectors to 3-D velocity vectors. (The manipulation of large arrays representing approximations to such functions is one of the main tasks of the Meteorological Office's supercomputers.)
Now I give a specific example of a velocity field that is useful for studies of perception in the control of robot and animal locomotion.
Suppose a camera attached to a robot is moving through the world. The image formed by the camera will be changing. If all the visible objects in the environment had closely textured high-contrast pattern on them, we could track the images of features of the pattern across the image plane of the camera. We can imagine drawing arrows on the image representing the speed and direction of motion of features at a given moment. If this set of arrows could be made very dense, so that an arrow could be associated with any point on the image plane, then we would have a 2-D vector field.
This field is closely related to what is known as the optic flow field for the moving camera.
In practice, an approximation to the image velocity field is easy to obtain by hand. You simply get two images from different positions of a camera (not too far apart), superimpose them, and join corresponding features with arrows. Each arrow effectively represents an image velocity vector.
In general, this velocity field will be a complex function like the wind field over Sussex - there is not a simple formula for it. However, under certain circumstances there is a good approximation which does obey a simple rule. If the following apply:
(a) the camera is viewing a smooth surface;
(b) the field of view is reasonably small;
(c) the camera is panned and tilted so that it tracks a feature at the centre of the image, which is taken as the origin for position;
then the image velocity field is approximately a linear function of image position. What this means is that if position in the image is represented by r and image velocity by v, the relationship is just a matrix multiplication:
v = M * r
where M is a 2x2 matrix. The 4 components of M depend on the direction the camera is moving and the slant and tilt of the surface. To write down this relationship is not trivial and will not be done here (references are available on request).
This example gives us another opportunity to look at the geometrical use of matrix multiplication. Particular combinations of components of the M matrix produce very different and distinctive image velocity fields.
Suppose, for example, that M is
- -
| 0.5 0 |
| 0 0.5 |
- -
Then it is easy to work out some examples of mappings from r to v:
r v
(1, 0) -> (0.5, 0)
(1, 2) -> (0.5, 1)
(0, -1) -> (0, -0.5)
etc.
Given such a table, it is easy to plot out some samples of the image velocity field as an arrow diagram. One naturally draws the arrow representing v at the position given by r, just as one would for the wind arrows on a meteorological map. If you do this for the table above and some more examples, you should get a picture looking roughly like
+ ^ +
\ | /
\ | /
(+ signs are arrow heads)
^
|
<----- <-- . --> ------>
|
v
/ | \
/ | \
+ v +
where the arrows get longer the further out from the origin you go. In other words, the diagonal matrix produces a dilating flow pattern.
This kind of flow pattern is generated by motion towards a surface.
Note the difference between this and matrix multiplication viewed as a transformation, as in FCS4 section 4. There, the idea was that a shape was mapped into another shape, or that a different coordinates system was used to represent the same shape. Here, a function from the position vectors maps onto a different kind of thing: a velocity. The actual matrix manipulations are, of course, the same, but their interpretation is different.
The effects of other forms of M are easy to calculate. You should be able to check, by calculating one or two vectors in each case, that
- - <--
| 0 -0.5 | produces something ^
| 0.5 0 | like: | . |
- - v
-->
This rotational flow field can be produced by spinning the camera about its axis. Note that the matrix is just 0.5 times the matrix for a rotation of 90 degrees (see FCS4, section 4.2), so it is not surprising that it has this effect.
The matrix
|
- - v
| 0.5 0 | produces something
| 0 -0.5 | like: <-- . -->
- -
^
|
which is one component of a shear field, and
- - -->
| 0 0.5 | produces something ^
| 0.5 0 | like: | . |
- - v
<--
which is the other component of shear. Shear flow fields are produced when a camera moves sideways in front of a slanted surface. For instance, the image of the ground in front of a mobile robot has the first component of shear combined with dilational flow, whilst the image of the ground to the side has the second component combined with rotational flow.
The details are not important; the point here is to illustrate the idea that a vector field, in this case generated by one of the simplest vector functions (multiplication by a matrix), can represent a rich variety of patterns - in this case patterns related to an important part of the perceptual process of a mobile agent.
In practice, the elements of the matrix have to be estimated from an image sequence. This can be done in a variety of ways, but typically a model, represented by the linear equation above, is fitted to the partial derivates of image intensity with respect to space and time coordinates. The matrix elements can then be used in a variety of ways, either to help build a 3-D representation of the environment, or more directly in a motor program.
You may be able to generate representations of flow patterns using a package such as Matlab. Alternatively, if you read TEACH FCS5 using the Ved editor, you can edit a small piece of code to generate pictures of flow patterns for any given matrix. For example, the matrix
- -
| 0 0.1 |
| 0.1 0 |
- -
generates the flow field representation shown here:
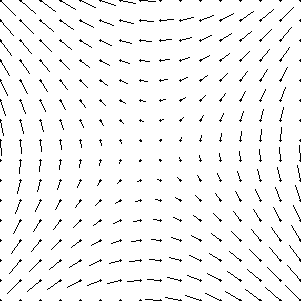
This program used does not draw the arrow heads, but puts a dot at the base of each arrow. The dots mark the positions corresponding to the r vectors.
A more complex example generated by the matrix
- -
| 0.1 -0.1 |
| 0.05 0.05|
- -
which produces a mixture of shear, dilation and rotation, appears as

A second application is to the control of robot arms. This will merely be outlined here to give the general idea; robot control textbooks give details and examples. I will also mention the use of alternatives to the Euclidean coordinate system.
Suppose a robot's gripper is operated from some base, and designed so that it can be moved on command to a given position above a plane, expressed in (x, y) coordinates, relative to that base. (Some piece of electronics on the base converts these coordinates to the signals which are actually sent to some motors to move the arm.)
gripper
O----------C
|
------+----
|^y | |
|| O | base
|-->x |
-----------
Provided there is a program that can work out the positions to send the arm to, there's no problem with this. However, the arm might not be able to reach everything that is needed, so it is mounted on a mobile base. The controller for this can turn it to face in any direction and can move it around the lab. Its position in the lab is also expressed in Euclidean coordinates, relative to some axes fixed to the floor, which will be denoted by (X, Y). The orientation of the base is indicated by an angle theta, which is the angle anticlockwise from the X-axis on the floor to the x-axis on the base. Thus we have something like
Y /
/ O----------C
/ | T target
/ ------+----
/ |^y | | mobile
/ || O | base
/ |-->x |
/ -----------
/
/
.
.
.
.
.
X .
(The dotted line is intended to represent the X-axis and should be at right-angles to the Y-axis.) Here theta is about 30 degrees. Note that it is independent of the base's position in the room.
The question is: if the position of an object in the room is specified in terms of its (X, Y) coordinates (i.e. its position on the floor), how do we move the gripper to it? Since the gripper control works in terms of (x, y), we need to work out where the target is relative to these coordinates. Although you could probably work out the answer using elementary geometry and trigonometry, the formula is very simple when expressed in terms of vector transformations. Suppose the robot's base (to be precise, the origin of its (x,y) coordinates) is at position B relative to the floor coordinate system, and the target is at position T in this coordinate system. What we need is the target's position in the base's coordinates, which we will denote by t. Then we can move the gripper directly to it, provided it is in range.
The formula to get from T and B to t is much simpler than the one you might work out using elementary mathematics. It is
t = R(-theta) * (T - B)
Here R(-theta) means the 2x2 matrix that rotates a vector anticlockwise through an angle -theta, or equivalently clockwise through an angle theta. The multiplication is a matrix-vector multiplication. From FCS4, section 4.2, we know that
- -
R(-theta) = | cos(theta) sin(theta) |
| -sin(theta) cos(theta) |
- -
(changing the signs, and remembering that cos(theta) = cos(-theta) and sin(theta) = -sin(-theta)). The formula is easy enough to evaluate in a computer program, possibly using library routines for the matrix operations.
You should be able to see why the formula is correct: T-B is the vector from the base to the target in the floor coordinate frame, and to express it in the base coordinate frame, which has been rotated anticlockwise by theta, the vector is in effect rotated clockwise by theta.
Why is this more useful than elementary geometry to do the same task? First, it is quicker and easier to write down and implement; provided you know what a rotation matrix looks like, or you know where to find out, you can have a procedure for the conversion set up in a few minutes.
Second, it is easier to manipulate. For example, we might want to go in the other direction. The robot might have a sensor on its base that detects the target and produces the components of t. We might then want to know T in order to plot the position of the object in a map that is being built of the lab. The equation can easily be reversed to yield
T = R(theta) * t + R
(by default, multiplications are always done before additions). This equation could be got either by reasoning about the situation, or simply by solving the first equation for T. Since R(theta) clearly reverses the effect of R(-theta), we can note in passing that R(-theta) is both the inverse and the transpose of R(theta).
Third, the method generalises better, in a variety of ways. The most obvious is to 3-D: the equations stay the same, though the rotation matrix becomes 3x3. It is also easy to incorporate additional links into the chain. For simplicity, we assumed that the gripper controller could simply move the gripper to given coordinates; in practice, this would be achieved by having several separate links in the arm. For each of these there is a coordinate transformation so that the target positition could be expressed in terms of that particular link's controller. For a chain of links, the equation for the target position can be applied recursively as information is passed along the chain - each link knows its own orientation relative to the previous one, and so can work out the target position in its coordinate system. And indeed, the coordinate systems that are used do not even have to have the same units, or have right-angles between their axes: these differences can be taken into account by using transformation matrices that are not pure rotation matrices. Then, the matrix inverse really comes into its own if the equations have to be solved to find the reverse transformations.
There are some tricks that are commonly used in this kind of computation. One important one is the use of homogeneous coordinates, which allow the operations in the equations above (a vector addition and matrix multiplication) to be carried out in a single multiplication step. This is done at the expense of including an extra element in the representation of each vector, and an extra row and column in each matrix. The extra vector elements are in fact redundant, but allow the vector to be added to be specified in the additional matrix elements. The technique will not be elaborated here, though it is not particularly difficult; it can speed up the algebraic manipulations needed for complex systems.
The central idea in this section is that of a frame of reference. Any physical vector must be expressed relative to such a frame but a given frame may not be suitable for all the operations that need to be carried out. Transformations between frames are therefore an essential operation.
So far, vectors have been represented using Euclidean (x,y) coordinates. It is often useful to represent them in other ways; one of the most common is polar coordinates. In 2-D polar coordinates, a position is represented by its distance from the origin (often denoted by r) and the angle a line joining it to the origin makes with the x-axis (often called theta). Such a coordinate system might be used because it corresponded better to the physical setup of a sensory or motor system; wherever there is a natural centre (such as the eye position in a visual system), polar coordinates merit consideration.
^
y | +
| /
| /
| /
| /
| / r
| /
| /
|/ <- angle theta
+-------------------------->
x
The relationships between polar and Euclidean coordinates are:
2 2
r = sqrt(x + y )
theta = +arctan(y/x) if x is positive
theta = -arctan(-y/x) if x is negative
assuming that arctan returns a result in the range -90 degrees to +90 degrees (or -pi to +pi radians). In the maths libraries provided with almost all computer languages there is a function, often called atan2, which does the theta calculation given y and x. This should always be used in preference to doing the division and calling atan or arctan explicitly.
To go in the opposite direction, use
x = r * cos(theta)
y = r * sin(theta)
Note that if a vector is expressed in terms of r and theta, the rules for addition and multiplication no longer apply. Essentially, you have to translate it to Euclidean coordinates before adding it to another vector by components or transforming it using matrix multiplication.
The transformation between polar and Euclidean coordinates is nonlinear because, for example, multiplying both x and y components by a constant multiplies r by that constant but does not change theta.
Often, however, it is necessary to transform small changes in a vector, represented in polar coordinates (or some other system), between coordinate frames. This might arise in the robot arm control system if we wanted to know what direction and speed the gripper will have relative to the floor if a motor somewhere in the middle of the arm is actuated at a given rate. A transformation of changes or velocities, can be carried out by a matrix multiplication without calculating the Euclidean coordinates. The elements of the matrix are derived from the coordinate relationships (they are actually partial derivatives), and such a matrix is known as a Jacobian matrix. Books such as that by Boas (reference in FCS1) go into considerable detail about this. Note that the inverse of the Jacobian (if it has one) may indicate how to activate the motors to produce a desired motion.
You may encounter the idea of linearising a problem by considering small changes in a quantity rather than the quantity itself. The use of the Jacobian matrix to calculate gripper velocities is a good example of this.
Polar coordinates can be extended to 3-D. Other forms of non-linear coordinate transformations can be found - for example log-polar coordinates are useful in some areas of vision.
Copyright University of Sussex 1997. All rights reserved.