
Looming and collision
During direct approach, immediacy
= 1/(expected time to collision)
= rate of dilation
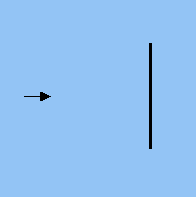

Problem
Dilation does not imply approach: it is also produced when the view angle changes


First-order flow
- Comprises dilation, shear and rotation.
- Is independent of pan/tilt eye movements.
- Is linear in image coordinates; we model the local flow with the first
two terms of the Taylor expansion
v(r) = v0 + M r + …
where v is the optic flow vector at image position r, v0 is the zero-order flow, and M is a 2×2 matrix of first-order flow parameters.

Dilation
- Expansion/contraction of image. Symbol D.
- Results from approach and from change of surface slant.

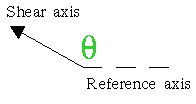
Shear
- Extension along a specified direction with contraction along the orthogonal direction. Symbols S (magnitude), theta (direction).
- Occurs during motion relative to a slanted surface.

Rotation
- Image rotation. Symbol R.
- Occurs during motion relative to a slanted surface; also produced by eye rotation about line of sight.

Example: rotation + shear

Goal
To understand the information available for the control of action from the instantaneous first-order optic flow of a single surface patch.
View general first-order flow mpeg or gif (dilation+rotation+shear).
"Action variables"
- We seek to generalise the immediacy-dilation relationship to 3D.
- We introduce 4 variables relevant to the control of action and determined by the flow.

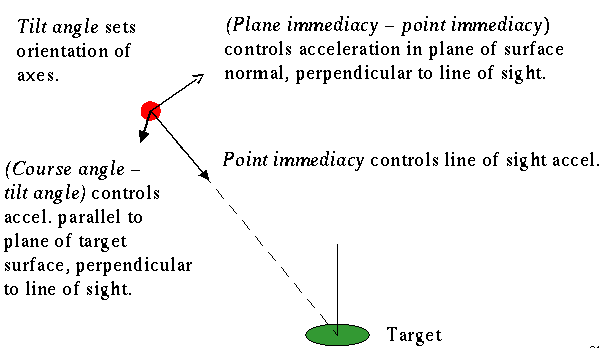
Plane immediacy
Inverse time to contact with plane containing surface patch (tangent plane).
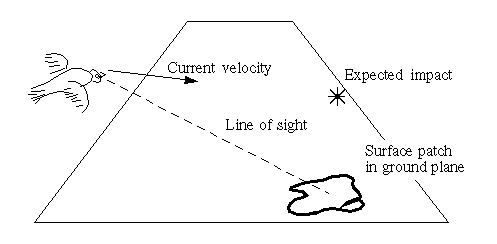
Plane immediacy and flow
Assume spin (physical rotation of visual system about line of sight) is 0.
Plane immediacy
= D - 3S cos(phi),
where sin(phi) = R/S

Point immediacy
Inverse time-to-contact with plane normal to line of sight and passing through point of interest (centre of patch).
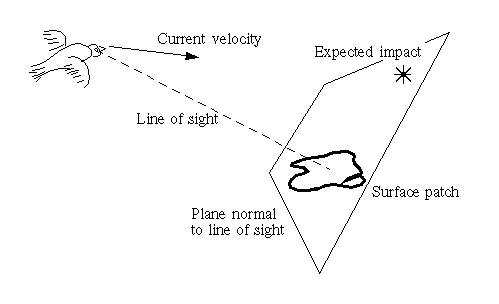
Point immediacy and flow
Assume zero spin.
Point immediacy
= D - S cos(phi),
where sin(phi) = R/S (as before).

Course angle
Orientation in image of plane containing line of sight and velocity vector.
Bird's eye view
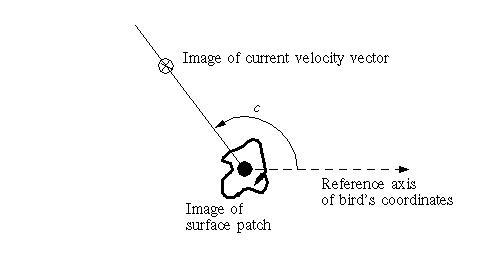
Course angle and flow
Assume zero spin.
Course angle
= theta + phi/2,
where sin(phi) = R/S

Surface tilt
The orientation in the image of the projection of the normal to the surface patch.
Bird's eye view
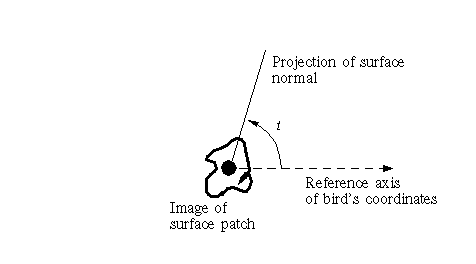
Tilt and flow
Assume zero spin.
Tilt angle
= theta - phi/2,
where sin(phi) = R/S

Action variables from flow
- If we can assume zero spin, then the first order flow determines the four action variables, up to two discrete ambiguities:
- you can add 180 degrees to the shear axis angle theta;
- you can replace phi by (180 degrees - phi).

Action variables for navigation
- We need to show that the four action variables are relevant to control.
- A theoretical demonstration is given by a simulated docking task.
An agent manoeuvring in 3D has to land on a surface patch gently, approaching along the surface normal.
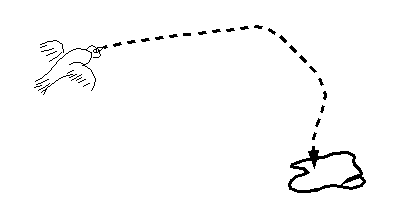

Rules for approach: a simple algorithm
View simulation mpeg or
gif.
Above: motion in two vertical orthogonal planes;
below: motion in horizontal plane, and optic flow

General form of the relations
Now phi couples the relations between the four flow variables D, R,S, theta and the five action variables, which now include spin.
- Independent measurement of any one of the action variables will constrain phi and hence all the other action variables (up to discrete ambiguities).
- E.g. in locomotion, plane immediacy for the ground plane might be known to be 0, or spin might be constrained.
- Other possible constraints include: flow from a second surface patch; second-order flow; variation of flow with time.
- Without any additional constraints, first-order flow from a single patch is unlikely to be useful.
| Plane immediacy | = | D - 3S cos phi |
| Point immediacy | = | D - S cos phi |
| Course angle | = | theta + phi/2 |
| Tilt angle | = | theta - phi/2 |
| Spin | = | R - S sin phi |

Possible experiments
Subjects can usually interpret first-order flow stimuli as arising from surfaces in 3-D motion.
- They can be asked to estimate action variables. Tilt and course angle are easiest.
- Since flow alone is ambiguous, the results of different assumptions — e.g. zero spin — can be compared with observations.

Conclusions
- First order flow from a single surface patch provides, in principle, powerful information for navigation in 3 dimensions — provided at least one additional constraint is present.
- Reformulating the relation between flow, surface orientation and motion makes it possible to ask experimentally how this information is used.