STEREO FLICKS

Until a very few years ago the only way to provide someone with a realistic 3-dimensional percept involved making them look at a specially prepared image through red/green specs. But this technique has now been superseded (to some degree) by the SIRDS or `Magic Eye' method. This enables a 3-dimensional percept to be presented without use of any special equipment. It is currently being used in the generation of a wide variety of images in many different media. Viewed raw, SIRDS or `integrams' as I call them, appear to contain nothing more than detailed, periodic patterns. But viewed with an offset vergence, they provide a rock solid, specs-free 3-d illusion.

In this file I will present some sample integrams and talk about how they can be constructed. I will also show a short `stereo flick'---a 3-dimensional movie made using the itegram method.

A encyclopaedic reference on stereograms is here.

Sample integrams

To get a 3-d percept from an integram it is necessary to make your eyes converge on a point behind the image. There are various ways of getting your eyes to do this. One method is to try to `look' at an imaginary object on the inside of the back-panel of your computer screen. Another method is to focus on your own reflection in the screen.

Here is a simple integram which features the letters `WO' floating above a plain, flat surface.

This next image contains a number of flat surfaces at various different depths.

This one contains a snaking, downwards sloping staircase.

Here's a black-and-white integram (useful for printing out).

You may find these example easier to see when they are blown up to the full size of the screen. You can do this by clicking on them to open up them up in the XV viewer and then clicking the top-left-corner button on the XV window to make it fill the screen.

Click here to run the `stereo flick'---a short video showing one surface moving vertically over another.

The year of the integram

Integrams trick the brain into perceiving 3-dimensional space that isn't really there. They do this by providing phoney `stereo cues' from which the brain derives phoney distance (depth) information. To understand how this works we need to understand a few basics about the visual system.

Animate visual systems use retinal arrays. These sense light falling on a roughly flat surface and thus deliver a 2-dimensional projection of the 3-dimensional world. Since organisms typically want to know something about the 3-dimensional properties of their world, they have to post-process retinal inputs so as to derive `depth' information, i.e., the real distances to the objects whose projections appear in the retinal array. If the organism has two eyes, this can be done quite effectively by

Solving the correspondence problem, i.e., working out which dot in one retinal image matches (i.e., originates from the same location as) which dot in the other retinal image, and then
Using disparities between matching dots to work out (by trigonometry) their true depth in 3-d space.

If this method is used it helps to have eyes which are close but not too close. This ensures the correspondence problem is not too hard (matching dots are not too far apart) and the trigonometry is not too inaccurate (significant differences in stereo disparity are derived from significant differences in vergence).

Settling on a a particular eye separation effectively `tunes' the visual system to stereo cues within a given depth of field (i.e., within given depth limits).

Traditional stereoscoping methods

To provide a stereoscopic visual system (i.e., a 2-eyed visual system which exploits stereo cues) with an `illusion' of a 3-dimensional scene, all you have to do is feed its left eye with the image that its left eye would normally get of that scene and its right eye with the image that its right eye would normally get of that scene. (These are of course identical except for the small disparities produced by the positional difference of the two eyes.) Through the years various methods have been developed for presenting such `stereo pairs' to the human visual system. An early method involved a contraption called the `Wheatstone stereoscope'. This was made of two, L-shaped viewing tubes which effectively fed a stereo pair of images to the viewer's left and right eyes. It looked something like this:

A better-known method involves the use of `red/green specs'. These are cardboard spectacles which cover one eye with a red filter and the other with a green filter. With these specs on, a viewer can obtain a 3-d image from a stereo pair drawn on a single surface, provided that one image in the pair is drawn in green and the other in red. The green image is effectively invisible to the green-covered eye and thus only gets to the red-covered eye, and vice versa.

The great advantage of the red/green specs method is that it enables the stereo pair to be presented on a single 2-dimensional surface, such as the page of a book or a cinema screen...

However, it also involves the viewer wearing the special spectacles. This is not ideal since what we would really like is to be able to produce 3-dimensional images on an ordinary 2-d surface without requiring the viewer to use any special equipment.

Intuition suggests that we shouldn't be able to do this. If we place our stereo pair on a single surface then the viewer's left eye will end-up seeing the dots in the right-eye's image and vice versa. But the insight underlying the integram method was that this wouldn't matter if those dots really were there in the right-eye's image. If the image can be somehow fixed up so so so as to ensure that whenever one eye sees the other eye's dot, that dot really is present in the first eye's image, the visual system will obtain a perfectly good stereo pair.

The idea sounds weird but it all boils down to a rather straightforward procedure for producing 3-d images. The basic idea is illustrated in the figure below. We imagine that we place the viewer's two eyes at one end of a rectangular frame. At the other end we place our chosen 3-dimensional surface and in between the two we place a blank, 2-dimensional image.

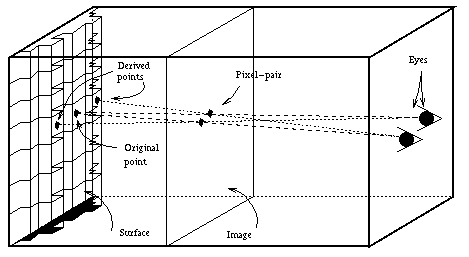To construct an integram of the surface we first place a coloured dot---a blue dot, say---at some arbitrary point on the surface. We then draw straight lines back from the dot to the viewer's two eyes placing two blue dots where the lines pass through the image. We have now constructed a stereo pair for the single blue dot. Of course the right eye will see the left eye's dot and vice versa. So we must now place blue dots on the surface point the right eye will interpret as being `responsible' for the left eye's dot, and the surface point the left eye will interpret as being responsible for the right eye's dot.

To complete the image we simply continue this procedure until the image is filled up. Each time we come across a surface dot that hasn't yet been coloured in, we assign it a random colour and carry on. The final image created is a fully integrated stereo pair. If it is viewed with a suitable vergence (i.e., with eyes converging on a point on the imaged surface) a full, 3-dimensional percept is obtained.

Micro and Macro Variants

The method described above is probably the simplest way of making integrams. It's main disadvantage is the fact that does not allow for image surfaces to be given any sort of coherent colouring. Thus the images produced are always of the `random dot' variety (hence the acronym `SIRDS' which stands for single-image random dot stereogram). However, it is possible to apply the method using real image features (i.e., faces, coins, fence posts etc.) rather than dots. This process is more complex since painting-up the image involves creating geometric `iterations' of the features used. However, it does allow for more realistic (i.e., non dotty) stereograms to be generated.

A dirt-cheap method for generating integrams is to take a sheet of white paper, select an alphabetic character and then iterate it with a given frequency (i.e., every 10 spaces) across the page. Move down a line or two and repeat the process using a slightly different frequency. When you have a page full of iteracted characters, try viewing the page in such a way as to fuse two neighbouring characters in the top row. If your spacing didn't fluctuate too wildly, all the lines of characters should fuse up too, but at different depths.

Remedies for poor fusing

Experience suggests that about 90% of people can learn to `see', integrams given a little practice. However, very few people seem to be able to see them straight away. For many people, the easiest way to deal with fusing difficulties is simply to view the image through a glass surface. By converging on his or her reflection, the viewer automatically converges on point `behind' the image and is thus in a good position to fuse the stereo pair.

One of the reasons fusing is hard may be that it involves making your visual system do something that it would never normally have to do, namely focus in one place while converging in another. Focussing on the image (while converging on the illusory surface) is essential if the image dots are to stay clear, unless the depth-of-field achieved by the visual system is sufficient to keep the dots clear even when the focal point is some way beyond the image. Thus difficulties in fusing may be to do with having poor depth-of-field or a lack of ability to `delink' focussing and convergence.

The almost insuperable problems people have in fusing integrams `back-to-front' suggests that depth-of-field may be the crucial factor. On the face of it, back-to-front fusing should be a perfect dual of the normal viewing process. The viewer converges on a point in front of the image rather than behind it (i.e., goes boss-eyed) thus inverting the geometry, making the surface appear to stick out in front rather than out the back. But back-to-front fusing is not a perfect dual of the usual procedure. It turns out to be very much harder! The theory that depth-of-field is crucial neatly accounts for this since the back-to-front fuser necesarily works at half the usual range, i.e., at a range where the depth-of-field is bound to be significantly diminished.

Imaging shortcuts

The imaging procedure described above illustrates the general character of the integram method. However it turns out that there is a way of generating integrams which does not involve doing any geometry. Rather than plotting the image intersections of surface-to-eye lines we simply iterate left-to-right, top-to-bottom over the surface assigning random colours to uncoloured dots. Each time we colour an image dot we colour in another image whose horizontal offset is linearly related to the depth of the surface immediately underneath the original image dot. Producing the image this way effectively skews the imaging frame (see diagram above) a little; however the process is substantially easier to implement.

The amount of computation involved in the imaging process can be reduced still further by effectively sub-sampling the surface, i.e., by leaving a certain amount of white space between dots. If sub-sampling is used, however, it is very important to ensure that occlusion effects are taken care of. If the image is generated in a naive way, simply by iterating left-to-right colouring in every Nth dot, then it is possible to end up with right-eye dots for points on the surface which are actually occluded (and would therefore be over-written in a non-sub-sampling procedure).

Whatever method is used, it is important to remember that the resolution of the image must be substantially higher than that of the imaged surface. The increase in resolution is needed to to take account of the fact that surface patches at different depths effectively project sub-frames of different size into the image. The image resolution must be sufficiently high to enable these different sub-frames to be accurately represented.

Open problems

The integram method (AKA SIRDS, or Magic Eye) is clearly an exciting and powerful way of generating images which give a real perception of depth. However, it is not quite the ideal method. To start with, all integrams whether they are of the micro (random-dot) or macro variety suffer from `fuzzy edges'. This is a result of the fact that the vertical margins of the image always contain surface features which have no stereo partners and thus cannot be visually fused. A second problem is the fact that, at present there seems to be no way to introduce proper colouring into micro (random-dot) integrams. In a left-to-right imaging process, the introduction of a dot in a particular colour results in that dot being `propagated' across the whole width of the image. Thus all colours end up being `splattered' all over the image. This is why integrams typically have a roughly uniform colouring.

LIB INTEGRAM

A simple, mouse-driven integram-generator is available to Sussex/COGS users. This can be run with the command

pop11 :lib integram

For further information see the Poplog help file HELP INTEGRAM.

Comments, suggestions etc. to Chris.Thornton@cogs.susx.ac.uk.

Misc. links

A collection of stereogram junk is here .

Other stereogram-related pages on the WWW include

A couple of journal papers of relevance are Christopher W. Tyler, The Birth of Computer Stereograms for Unaided Vision, STEREOGRAM, Boxtree, 1994; and How to Play Tricks with Dots, in NEW SCIENTIST, 9 October, 1993.

Page created on: Fri Apr 26 09:58:12 BST 2002
Feedback to Chris Thornton

hits this year