The Replex

r e p l e x . . .

New work in the Creative Systems Lab at the University of Sussex is exploring the `replex', an informationally-defined entity with applications in generative music. A replex is a machine-generated sequence which `copies' the informational properties of some existing sequence. In simple cases, replexes can be simple, syntactic variants. For example, XXYZZ is a not very surprising replex of AABCC. In other cases, they may show more differences. This has interesting implications where the original sequence is a story, a poem or some music. In this situation, a replex might show a combination of superficial differences and structural commonalities, enabling it to `inherit' some of the aesthetic properties of the original. (Technical information on definitions and derivation methods is available here.)

As an illustration, consider this replex derived from the opening bars of of Beethoven's `Fur Elise'. Press Play to start playback. Press Stop to finish.

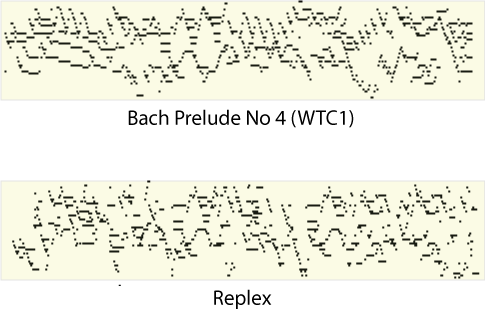This longer replex is derived from Bach's prelude No. 4 in C# minor (from WTC Book 1). The image on the right contrasts a note-grams for this piece with one for the original.

For comparison, the original composition sounds like this.

Comparing replexes with their sources, you may be able to hear patterns from one cropping up in the other. Different types of music produce different degrees of this. Music with more intricately repetitive structure (e.g., Baroque piano music) will have more elaborate informational properties. This tends to yield more organized replexes and more obvious inheritance effects.

This replex is derived from the final bars of the 1st movement of Stravinsky's Symphony of Psalms.

This replex is derived from Bach's Fugue no. 5 from WTC2 (bars 13-63).

This is derived from parts of Scarlatti's sonata in C minor (k11).

r h y m e s . . .

Replexes can also be derived from textual sequences such as speeches, stories, jokes and poems. Consider the traditional nursery rhyme `For want of a nail'.

For want of a nail the shoe was lost.
For want of a shoe the horse was lost.
For want of a horse the rider was lost.
For want of a rider the battle was lost.
For want of a battle the kingdom was lost
and all for the want of a horseshoe nail.

The prominent, repetitive structure here yields quite good replexes, as illustrated by the text-box below. The text here is generated by an applet that will generate a new replex each time you click anywhere in the window. The replex may or may not differ from the original. Any sequence is automatically a replex of itself. There's always a chance that replex-generation will regenerate a perfect replica. In most cases, there are a very large number of possible replexes, meaning that re-generation of the original source is highly unlikely. (The total number of replexes in a given case can be calculated by measuring the branching factor of the relevant information structure---see below).

As in the case of musical replexes, the greater the degree of statistical structure in the source, the more likely it is the replex will exhibit recognizable variations. Replexes derived from texts with complex, interwoven patterns tend to be have more obvious organization. This effect is illustrated with this replex-generator which uses items 6-10 from the Ten Commandments.

If you skip down a few sections, you'll find a detachable applet which you can use to generate your own text replexes.

h y p e r - r e p l e x e s . . .

For generative work with replexes, the simplest approach is to focus on complete sources, i.e., whole pieces of music, complete stories etc. This keeps things simple. We can give a straightforward account of the thing we have derived a replex of. But it doesn't have to work like this. We can derive information structures for part works or combinations of works. The latter approach, in fact, is the easiest way to construct a `multi-replex', i.e., a seguence derived from several sources.

A more powerful method involves using an amalgamation of information structures of several sources. Instances generated from amalgamated information structures are `hyper-replexes'.

hyper replexes here...

f u z z y - r e p l e x e s . . .

Another interesting possibility is the `fuzzy replex'. This is a sequence which embodies some statistical randomness or `noise'. There are several possibilities for adding noise to replexes, including the obvious scheme of simply randomizing symbol substitution process during reconstitution. A more interesting idea involves adding noise just to the lower level elements in a reconstitution, i.e., those elements which have been derived from the more fine-grained components of the structure. To generate this sort of object, we intervene in the expansion process so as to ensure that below a certain depth, the ordering of data is random. Sequences derived may then inherit higher-level structural properties to a greater degree than lower-level ones.

a p p l e t . . .

For experimentation with replexes we need software that can apply sequence reduction to sequences and then perform reconstitution using derived information structure.

The `replexer' applet (button below) provides this functionality for text sequences. In the window that pops up you'll see some buttons on the left, with small windows above and below. Next to this, there are two long windows. To run the program type (or paste with CTRL-V) some text into the upper-left window. Then press the Analyze button. The system will apply sequence reduction to the text and display the results in the form of an information structure (right window) and an interpretation hierarchy (middle window). In the middle display, it is possible to see how symbols in the initial sequence have been relabeled, incrementally reducing the sequence to a single element.

To generate a replex of the source, press the Make button. A reconstituted variant will then be constructed and displayed in the bottom-left window.

c o n n e c t i o n s . . .

Replex analysis borrows from a variety of sources and also suggests some new angles on old problems.

Derivation of information structures for sequential data can be viewed as a form of sequence analysis. This application has become increasingly significant in recent years as a result of the need for better interpretation of DNA data. On the assumption that nature probably uses DNA in an informationally efficient manner, there is the possibility of DNA analysis based on identification of information structures.
Derivation of information structures can also be viewed as a type of data compression. Common compression methods (such as LZW compression) build encodings for sequential data by constructing labels for subsequences, in a similar fashion to sequence reduction. However the encodings generated are not usually hierarchical or informationally optimal.
Music-generative methods often use Markov chaining, a method which chains musical events together so as to conform to transition probabilities observed in some database of examples. The process is like sequence reduction in its exploitation of sequential redundancy (i.e., `fuzzy repeats'). But, being non-hierarchical, it has to be directed towards effects at a specific level of detail. There is the possibility, then, of adapting sequence reconstitution to provide a hierarchical generalization of Markov-chaining.
Where sequence reduction is applied to natural language sequences, groupings often correspond to syntactic or semantic categories. This is apparent with the `george1' and `simpsons1' examples accessed from the applet. The information structure for the latter (shown on the right) contains constituents corresponding to all the main syntactic categories evidenced in the data, including proper names, nouns, verbs, verb phrases and noun phrases. There is the possibility of adapting sequence reduction as an informational form of grammatical inference.
Where musical compositions are used as data for (information-structure) analysis, the process can also be viewed as learning, with the supplied data then being seen as `examples'. On this view, an interesting aspect of sequence reduction is its ability to perform `one shot learning', i.e., to produce output on the basis of a single example.
Traditionally, there have been two main areas of information theory. The Shannon version of the theory is based on the idea that the amount of information in a signal or event is the degree to which it reduces uncertainty in an observer. The Kolmogorov version of the theory ( Algorithmic information theory) is based on the idea that the amount of information in a structured object is the size of its smallest effective description. However, it is only Shannon information which can be measured in general. In calculating the information hiearchy of a sequence, we are evaluating informational properties of a structured object but doing so using Shannon's approach. Alternatively, we might see it as calculating a type of Kolmogorov complexity where `the computer' is equated with the functionality of symbol-rewriting.
The Kolmogorov connection also connects sequence reduction with inference. Kolmogorov's idea (that the amount of complexity in some data is the size of its smallest generative description) is closely related to Occam's Razor, the principle that the best model for some data is also the simplest that can be devised. This in turn is related to the idea that it is the simplest model which generates the best inductive inferences and generalizations. A well-known incarnation of this is Rissanen's Minimum Description Length (MDL) principle, which states that the best model of some data is the one that provides the largest compression of the data. Rissanen's approach is particularly relevant since it specifically relates to sequential encodings (hence the `length' in the title). However, it does not dictate the way in which encodings are derived and it does not naturally accommodate hierarchical reduction. Nevertheless, there is a a close relationship and there may be the possibility of treating sequence reduction as an MDL variant which is `automatic' (i.e., code-inventing) and hierarchical.

c o p y r i g h t . . .

As the examples on this page show, replex-derivation can produce variations and combinations of existing musical and textual sequences. But where the original sequences are valued artefacts (such as Bach preludes) there is the problem of deciding who has copyright on the generated example. In an informational sense, any replex is identical to its source. So where there is a single source, this would seem to dictate that the the copyright for a replex should rest with whoever has copyright on the source. But this goes against the convention that copyright does not extend to artefacts which vary an original in any kind of substantial way. And it doesn't work with multi-replexes. Perhaps the best that can be said is that replex analysis challenges conventions on copyright.

m o r e . . .

For further information, examples, software, sources etc., contact Chris Thornton at sussex.ac.uk (using initial.lastname).

Feedback and comments welcome.