Machine Learning - Lecture 7: Information Theory

Chris Thornton

Introduction

Machine learning involves modeling data for purposes of predicting variable values.

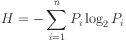
We've looked at some of the ways we can measure the performance of supervised learning on a particular task, e.g., through calculation of error rate.

Is there any general way of working out how good a model really is?

Can we measure how much knowledge it contains?

Concepts of information theory are of use here.

Information theory

This framework was put together (as an MSc dissertation) by Claude Shannon in the late 40s. The most accessible publication is

The ideas in the theory revolve around quantification of uncertainty.

This becomes a way of working out how much is already known in a particular situation, and therefore how much can be learned from new data.

Uncertainty example

Say you get a txt from a friend suggesting meeting by the pier. You're not sure if this means the palace or west pier.

Your actual level of uncertainty depends on the probabilities you give to the two possibilities.

The best case is where you can give all probability to one case:

  P(palacePier) = 1.0
  P(westPier) = 0.0
The worst case is the 50/50 situation where 

  P(palacePier) = 0.5
  P(westPier) = 0.5
Semi-flat distributions express intermediate amounts of uncertainty.

Uncertainty increases with the flatness of the distribution applied.

Taking the number of possibilities into account

The other factor that influences the level of uncertainty is the total number of possibilities.

If the txt suggests meeting outside the cinema, you'd then have three possible interpretations: Odean, Cinecentre and DoY.

Someone faced with three equally probable alternatives has to be more uncertain than someone faced with two equally probable alternatives.

So the total number of alternatives must also contribute to level of uncertainty.

Shannon's insight

It seems a valid way of measuring uncertainty must do two things:

  1. It must give bigger values for flatter distributions.

  2. It must give bigger values for broader distributions.

Shannon showed there's just one formula that works like this, and it's the entropy formula.

Entropy formula

The entropy formula looks like this:


This defines entropy (H) to be the result of multiplying each probability by the log of itself, summing all the results and taking the negative of the result.

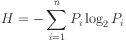
It's not necessary to understand why or how this works. (Although you may need to implement it in Java.)

The point to remember is that this calculation meets the requirements for an uncertainty measure: its values get bigger with both the flatness and range of the probability distribution .

From uncertainty to information

An a resercher for Bell Labs, Shannon had telecommunications particularly in mind.

He was interested in the possibility of quantifying amounts of information.

He proposed that we can quantify information in terms of reduction of uncertainty.

Using this idea, it becomes possible to measure the amount of information conveyed by signals.

We can also use the idea to evaluate coding schemes.

Optimal digital codes

If the txt specifies meeting at a `station', our probability distribution might be completely flat:

  P(Brighton) = 1/4
  P(PrestonPark) = 1/4
  P(Hove) = 1/4
  P(LondonRoad) = 1/4
The entropy for this, with logs taken to base 2, turns out to be exactly 2.0.

Spot the coincidence.

Uncertainty identifies how many questions are needed

With logs taken to base 2, the value we get back is the number of 2-way questions we need to specify a particular outcome, i.e., one of the four stations.

It's also the number of binary digits we need to represent four different cases (which is really the same thing).

An optimal digital code to represent the four stations is thus found to use just two binary digits.

It doesn't have to be binary

This rule works with all bases, and all forms of distribution.

(What would we get for the stations distribution if we calculate entropy with logs taken to base 4?)

The one niggle is the likelihood of getting back a non-integer entropy when we have a distribution that is not perfectly flat.

In this case, we have to round up to get the required number of questions/digits.

Redundancy

Using this way of working out a required number of digital codes, we can also assess redundancy.

A coding scheme is said to be redundant if the number of codes deployed is more than the number required.

The amount of redundancy is just the number of surplus codes used.

Origin of `bits'

Why all the talk of `bits'?

Working information values out, we usually work on the basis of logs measured to base 2. The digits identified through entropy measurement then have 2 values; information theorists call them `bits', as a contraction of `BInary digiTS'.

We need just 2 binary digits (bits) to specify one of four stations.

If we were to use 3 binary bits, we would then have 1 bit of redundancy.

(Note: `bits' in information theory are slightly different from `bits' in computer science.)

Putting it together

When we use a ML method to obtain a model, we're seeking a way to predict values of certain variables.

But the predictions forthcoming will always be uncertain to some degree, i.e., they will be probabilistic in nature.

Information theory then offers a way of assessing the general quality of the model, as a `store of knowledge' about the data.

The amount of uncertainty elimianted by a model quantifies the knowledge it encapsulates.

Information-theoretic measurements can be a way of guiding and evaluation model construction.

The next two lectures will look at a useful application of this idea.

Summary

Questions

More questions