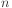 chunks
and train
chunks
and train 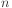 times, treating a different chunk as the
holdout set each time.
times, treating a different chunk as the
holdout set each time.
But this generic task is broken down into a number of special cases.
We also have a range of ways in which the performance of methods is assessed and described.
This lecture will examine some of the concepts involved.
The to-be-predicted variable is called the output variable.
Correct values of the output variable are called target output values, or just targets.
If the output variable takes categorical values, it may be called the class variable, in which case targets may be called target classes.
In some cases, there may be multiple output variables, but this is quite unusual.
Their values are input values.
If they take categorical values, they may be called attributes or features.
Their values are then attribute values or feature values.
A complete set of input values may be called a vector, attribute vector or feature vector.
Confusingly, input vectors are also sometimes just called inputs.
Any other scenario is then some form of unsupervised learning.
However, the latter term is usually reserved for the case where a model is built without any pre-classification of variables.
If the values are real numbers, the task is called regression.
A simple but popular case of classification is concept learning.
This is where the aim is to predict whether an input vector is or is not a member of a particular class.
Values of the output variable in this case are usually given as +/-, 1/0, or yes/no.
We then usually have a second set of examples, called the testing set, which is used solely for testing generalization performance, i.e., ability of the model to produce correct output values for input vectors that do not appear in the training set.
Cases in the training set may be called training examples.
Statisticians are more likely to call them seen cases, or just seens.
Cases in the testing set may be called testing examples, unseen cases or just unseens.
The inaccuracy of predicted output values is termed the error of the method.
If target values are categorical, the error is expressed as an error rate.
This is the proportion of cases where the prediction is wrong.
It may also be called the prediction error-rate, or generalization error-rate.
If error is calculated on the training set, then it would be called the training error-rate.
petrol hatchback FW-drive Ford diesel saloon FW-drive Ford petrol formula-1 FW-drive Ferrari petrol convertible FW-drive FordThe testing set has two cases:
petrol convertible RW-drive diesel hardtop FW-driveUsing a 1-NN method, both inputs are classified as Fords.
However, it turns out that the first case is in fact a Ferrari.
The model gets 1 out of 2 classifications wrong.
The error rate is 50%.
On the other hand, we need to be sure that both sets of data originate from the same source or domain.
If they don't, there's no reason to expect that a model built for one will apply to the other.
In ML, we normally handle this by requiring the training and testing data to be identically and independently distributed.
It is a requirement that the testing data show the same statistical distribution as the training data.
But they must also be completely independent of the training data.
This is known as the IID assumption.
A holdout set is a (usually) small set of input/output examples held back for purposes of tuning the modeling.
The modeling process gets to see all the training data in the usual way.
But it then gets tested on the cases held back and the performance measurements obtained are used to control the modeling in some way (e.g., set a parameter).
Note that this is completely separate from use of a testing set, which is used for obtaining a final evaluation.
For example, we might hold back 10% of the training data and try to find the optimal value of k in k-means clustering by seeing which value gives the lowest error-rate on the holdout data.
But the evaluations obtained in this case tend to reflect the particular way the data are divided up.
The solution is to use statistical sampling to get a more accurate measurments.
This is called cross-validation.
The basic protocols are
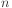 chunks
and train
chunks
and train 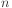 times, treating a different chunk as the
holdout set each time.
times, treating a different chunk as the
holdout set each time.