
KR-IST Lecture 9a Bayesian networks
Chris Thornton
Bayes rule again
Given evidence E and some conclusion C, it's always the case that
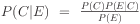
We can plug any values we like into this formula to infer the
probability of the conclusion given the evidence.
Lecture attendance example
So, from
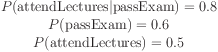
we can use Bayes rule to calculate probability of passing the exam:

The probability of passing the exam given you attend lectures is
0.96.
Complex Bayesian reasoning
Bayes' rule provides a single step of probabilistic backwards
reasoning.
This works for simple scenarios, e.g., where we have a
lot probabilities relating diseases to symptoms, and
want a rule that produces a diagnosis from the symptoms
shown.
But in more complex cases, we may have a networks or chain of probabilistic
relationships to deal with.
For example,
cheapMoney => consumerBorrowing => highDemand => inflation
How do we represent and perform inference with complex chains of this sort?
Answer: Bayesian networks
Probabilistic representation
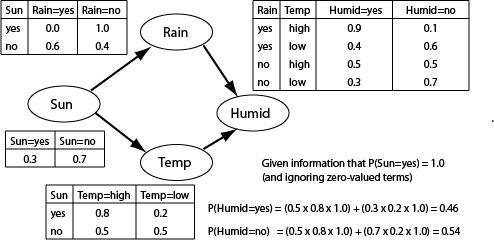
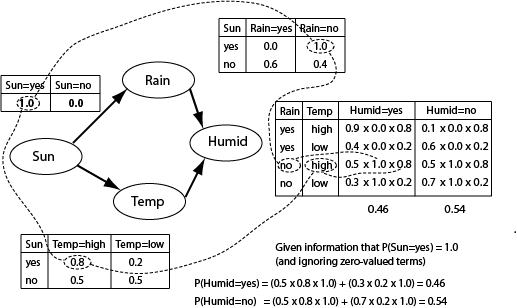
Let's say we want to work out if it's going to be humid tomorrow.
We have a tangle of relationships to take into account. Sunshine
increases the humidity but so does rain and temperature, both of
which are themselves affected by sunshine.
- Represent each element of the domain as a variable which takes
certain values (e.g., sun=yes, sun=no).
- Represent the relationships between variables in terms of
conditional probabilities, e.g., probabilities like
P(temp=high|sun=yes) = 0.8, P(temp=high|sun=no) = 0.2,
P(rain=yes|temp=low) = 0.6 etc.
Apply the laws of probability
To find out if it's going to be humid, start with some variables
that we know the value of and work forwards, establishing the
probability distribution on one variable by taking into account all
its conditional probabilities and all the (distributions on) all
the variables which those probabilities depend on.
This is also known as forwards propagation.
Bayesian network
Draw out the network of conditional relationships and annotate
nodes with the CPTs (conditional probability tables).
Reasoning as propagation
Terminology and assumptions
In Bayesian networks, any variable 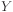 which has a direct
influence on variable
which has a direct
influence on variable 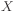 is said to be
is said to be 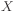 's parent.
's parent.
An arrow points from parent 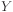 to
to 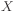
Variable 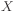 is then said to be
is then said to be 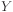 's child, while
's child, while
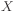 and all
and all 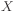 's children are
's children are 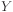 's descendants.
's descendants.
When reasoning is done using probability propagation, the
assumption is made that two variables are conditionally
independent of all non-descendants given their parents.
This is another way of saying that variables are only influenced
by their parents.
Top-down/forwards propagation
To find the probability of the ith value of variable 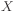 ,
use
,
use
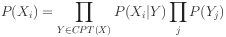
This defines the distribution on 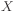 recursively.
Each value is obtained by iterating over the
combinations of parental values taking the product of
the combination's probability and the probability of the
value which is conditional on the combination.
recursively.
Each value is obtained by iterating over the
combinations of parental values taking the product of
the combination's probability and the probability of the
value which is conditional on the combination.
Termination
Termination is achieved by providing a non-conditional
distribution for some root variable.
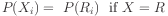
Note that distributions must sum to 1 (so normalization may be
required).
How well does it work?
Reasoning using Bayesian nets works perfectly in the
sense that probabililies are consistently propagated.
But depending on how variables are related, we can
easily end up with very uncertain conclusions.
The key factor which affects performance is the level of
uncertainty we have about conditioned variables.
This is the termed equivocation.
Equivocation formula
To calculate the equivocation of a conditioned variable
relative to a conditioning variable, derive the weighted
average of the uncertainties (entropies) of conditional
distributions.
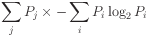
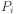 is the conditioned probability of the ith value of
the conditioned variable, and
is the conditioned probability of the ith value of
the conditioned variable, and 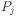 is the probability of the
conditioning value.
is the probability of the
conditioning value.
Equivocation as a weighted uncertainty sum
Equivocation is really just a weighted sum of the uncertainties of
the conditional distributions.
Other things being equal, higher equivocation will mean less
successful Bayesian reasoning, i.e., less certain conclusions.
.
Summary
- Bayes rule again
- Probabilistic representation
- Use of Bayesian networks
- Reasoning as propagation
- Top-down propagation
- Equivocation
Questions
- Let's say the university communicates your degree
result to you using either a tick or a cross. What is
the level of equivocation?
Exercises
- Use Bayes' rule to work out P(east|sun) given that
P(sun)= 0.3, P(east)=0.4 and P(sun|east)=0.6.
- Use the frequency interpretation of probability to explain
why Bayes rule works.
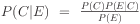

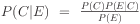
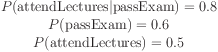



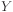 which has a direct
influence on variable
which has a direct
influence on variable 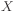 is said to be
is said to be 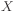 's parent.
's parent.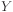 to
to 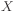
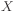 is then said to be
is then said to be 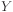 's child, while
's child, while
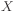 and all
and all 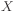 's children are
's children are 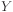 's descendants.
's descendants.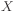 ,
use
,
use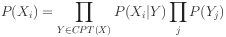
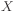 recursively.
Each value is obtained by iterating over the
combinations of parental values taking the product of
the combination's probability and the probability of the
value which is conditional on the combination.
recursively.
Each value is obtained by iterating over the
combinations of parental values taking the product of
the combination's probability and the probability of the
value which is conditional on the combination.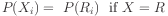
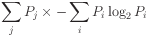
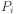 is the conditioned probability of the ith value of
the conditioned variable, and
is the conditioned probability of the ith value of
the conditioned variable, and 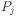 is the probability of the
conditioning value.
is the probability of the
conditioning value.