KR-IST Lecture 8b Bayesian Reasoning

Chris Thornton

From rules to conditional probabilities

The standard symbolic rule is treated as fully certain.

speedingTicket speeding

This is read `getting a speedingTicket implies that you were speeding'.

But we often need to be able to state consequences probabilistically. This can be done using conditional probabilities.


This is read `the probability of speeding given that you got a speeding ticket is 0.9'

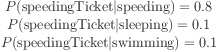
Conditional probability distributions

Working in terms of conditional probabililties, we have a distribution of probability values over possible states of affairs.


Probabilities in a distribution must sum to 1.0.

Uncertainty

The level of uncertainty regarding the state of affairs can be worked out by looking at the distribution.

The more flat it is, the greater the uncertainty.

The more cases there are, the greater the uncertainty (for distributions of a particular flatness).

Entropy

The entropy formula takes both aspects into account.


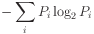
where 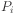is the probability of the ith alternative.

The value of the entropy rises with the number of alternatives and the uniformity of the attributed probabilities.

More extreme probabilities produce lower evaluations.


Information and knowledge

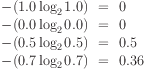
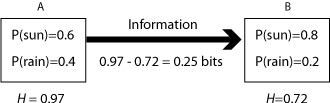
Using entropy as a measure of uncertainty, we can evaluate how much information is obtained when something happens (e.g., a message) which updates distributions.

Reduction of uncertainty implies an increase of knowledge.

Information in bits

Let's say there are 4 possible states of affairs: speeding, sleeping, swimming, eating.

We have no knowledge about which is the case.

The probability distribution is {0.25, 0.25, 0.25, 0.25}.

The entropy is 2.0

(It's always 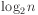with a flat distribution.)

Given we took logs to base 2, the entropy is also the number of bits you need in a binary system to encode 4 values.

The amount of information in a message or event which establishes the state of affairs is then measured as 2 bits.

Probabilistic reasoning

As well as being key for information theory, conditional probabilities are also the basis for methods of probabilistic reasoning.

These methods chain implications together in a way that takes probability into account.

The simplest approach to probabilistic reasoning uses the inference method known as Bayes' rule.

Bayes rule

Given evidence E and some conclusion C, it's always the case that


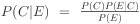
We can plug any values we like into this formula to infer a conditional probability for the conclusion.

P(C) and P(E) are called prior probabilities. P(E|C) is the likelihood. P(C|E) is called the posterior probability.

Rich bankers example

Flu diagnosis example

Exam prediction example

Bayesian (MAP) inference

Say we have observations D1, D2, and explanatory hypotheses H1 and H2, with all priors (e.g., P(D2)) and likelihoods (e.g., P(D2|H1)) known.

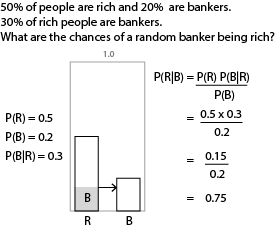
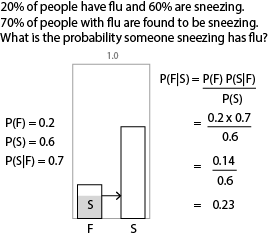
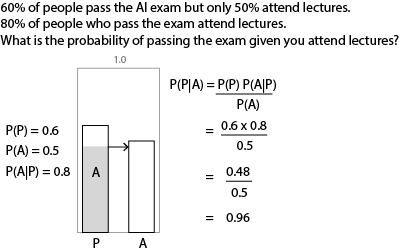
By combining Bayes rule with the product rule, can find the probability of each hypothesis given the data.

P(H1|D1,D2) = P(H1|D1) x P(H1|D2)

The most probable hypothesis is called the maximum a posteriori (MAP) hypothesis.

Deriving it is called MAP inference (what is usually meant by `Bayesian inference')

In practice, the process has the problem that probabilities become vanishingly small.

Summary

The classic texts