


The combination of rulebase and inference method can be viewed as a representation of knowledge for the domain, i.e., a knowledge base (KB).
A system which packages up knowledge represented this way is a knowledge-based or expert system.
With a history stretching back 2000 years, the study of logic and formal reasoning was a kind of pre-computation AI.
AI methods of knowledge representation (KR) are generally based on adapted systems of formal logic.
Allows facts about the world to be represented as sentences formed from:
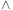
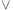


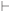
 P
P
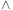 Q)
Q)
 R
R
A truth table shows how truth values combine under the relevant relationship.
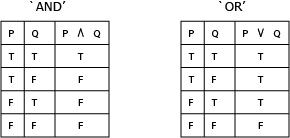
P  Q
Q
P
 Q
Q
P  Q
Q
 Q
Q
 P
P
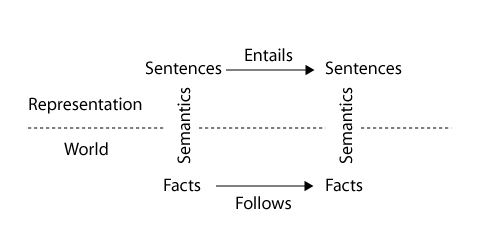
This is normally a truth value, i.e., true or false.
The associated inference method is then said to be
The way one fact follows another should be mirrored by the way one sentence is entailed by another.
We cannot represent property-based generalisations.
For example, it is impossible to represent this categorical syllogism in Propositional logic:
Every person is mortal
Tony Blair is a person
Therefore Tony Blair is mortal
 at least
one X such that...
at least
one X such that...
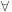 X it is the
case that...
X it is the
case that...
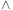 likes(alison, chocolate)
likes(alison, chocolate)
 likes(alison, richard)
likes(alison, richard)
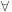 X: elephant(X)
X: elephant(X)  grey(X)
grey(X)
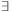 X: alligator(X)
X: alligator(X) 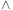 white(X)
white(X)
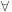 X:
likes(alison, X)
X:
likes(alison, X)  eats(alison, X)
eats(alison, X)
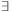 X: bird(X)
X: bird(X) 
 flies(X).
flies(X).
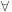 X:
person(X)
X:
person(X) 
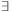 Y: loves(X,Y)
Y: loves(X,Y)
Consider these
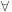 x: gardener(x)
x: gardener(x)  likes(x,Sun)
likes(x,Sun)
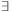 x: (person(x)
x: (person(x) 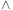
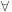 t: (time(t) =>
can-fool(x,t)))
t: (time(t) =>
can-fool(x,t)))
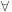 x: (person(x)
x: (person(x) 
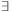 t: (time(t)
t: (time(t)
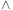 can-fool(x,t)))
can-fool(x,t)))
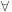 x: (mushroom(x)
x: (mushroom(x)
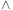 purple(x))
purple(x))  poisonous(x)
poisonous(x)

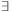 x: purple(x)
x: purple(x) 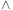 mushroom(x)
mushroom(x) 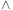 poisonous(x) or, equivalently,
poisonous(x) or, equivalently, 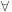 x:
(mushroom(x)
x:
(mushroom(x) 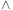 purple(x))
purple(x)) 
 poisonous(x)
poisonous(x)
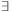 x
x
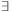 y: mushroom(x)
y: mushroom(x) 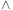 purple(x)
purple(x) 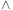 mushroom(y)
mushroom(y) 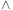 purple(y)
purple(y) 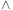
 (x=y)
(x=y)
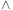
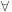 z: (mushroom(z)
z: (mushroom(z) 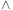 purple(z))
purple(z))
 ( (x=z)
( (x=z) 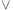 (y=z) )
(y=z) )
 tall(Deb)
tall(Deb)
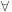 x
x 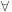 y: above(x,y)
y: above(x,y)
 (on(x,y)
(on(x,y) 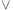
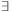 z (on(x,z)
z (on(x,z)
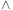 above(z,y)))
above(z,y)))
But its expressiveness complicates the derivation of inferences. (It gets easier if we exliminate existential quantification and assume `negation by failure'.)
Also, in FOL you cannot construct sentences which make assertions about other sentences. For example, you cannot say things like `there exists a property such that...'
For this task, you need a higher-order logic.
For example
This affects all varieties of knowledge representation but is particularly apparent where evaluation is in terms of truth, and rules are used to define the results of actions.
paint(X, C)  color(X, C)
color(X, C)
move(X, P)  position(X, P)
position(X, P)
and it is known that
paint(tony, blue).
move(tony, garden).
We should then be able to infer that
colour(tony, blue) 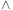 position(tony, garden)
position(tony, garden)
But the inference is, in fact, logically unsound
There is the possibility that the colour of tony gets changed by the move action.
Nothing in what we know rules this out.
Such rules are known as frame axioms.
For example
move(X, P) 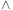 color-before-move(X, C)
color-before-move(X, C)  color(X, C).
color(X, C).
asserts the fact that moving an object will not affect its colour.
However, this is not satisfactory.
Since most actions do not affect most properties of a situation, in
a domain comprising  actions and
actions and 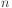 properties, we are going
to need approximately
properties, we are going
to need approximately 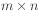 frame axioms.
frame axioms.
Imagine being the designer of a robot that has to carry out an everyday task, such as making a cup of tea. Now, suppose the robot has to take a tea-cup from the cupboard. The present location of the cup is represented as a sentence in its database of facts alongside those representing innumerable other features of the ongoing situation, such as the ambient temperature, the configuration of its arms, the current date, the colour of the tea-pot, and so on. Having grasped the cup and withdrawn it from the cupboard, the robot needs to update this database. The location of the cup has clearly changed, so that's one fact that demands revision. But which other sentences require modification?
Every knowledge representation is formal
Propositional logic is a knowledge representation
Therefore propositional logic is formal
There is a house in New Orleans
They call the Rising Sun
And it's been the ruin of many a poor boy
And God I know I'm one
My mother was a tailor
She sewed my new bluejeans
My father was a gamblin' man
Down in New Orleans
Now the only thing a gambler needs
Is a suitcase and trunk
And the only time he's satisfied
Is when he's on a drunk
To be considered for the best mortgage deals during the current
difficult conditions, you must borrow substantially less than the
full purchase price, have a perfect credit record and be able to
act fast.
Only people who have built up savings over
several years and have shown their ability to live on less than
their salary are able to get a mortgage.
It is first-time buyers who are hardest hit by the need to stump up
a bigger deposit in order to get the choice of the best deals.
When a man loves a woman
Can't keep his mind on nothing else
He'll trade the world
For the good things he's found
If she's bad, he can't see it
She can do no wrong
Turn his back on his best friend
If he put her down
When a man loves a woman
Spend his very last time
Tryin' to hold on to what he needs
He'd give up all his comfort
Sleep out in the rain
If she says that's the way it ought to be