Frequently Asked Questions

 

This section brings together some of the questions that have been frequenlty asked about logic over the past few years. Follow the links to get answers and pointers.

 

Do I need to learn the truth matrices for all the logical connectives?

Yes,  but you shouldn't be too concerned, as it isn't difficult to remember them. Here is a summary of the different connectives for the Propositional Calculus and their truth-functional definitions:

NOT -
t f
f t
AND t f
t t f
f f f
OR t f
t t t
f t f
IF t f
t t f
f t t
IFF t f
t t f
f f t



The truth matrix for implication says that A -> B will be true whenever A is false -- surely that can't be right can it?

Don't forget that we are dealing here with classical logic. This means that any statement must be either true or false, it cannot be undefined and it cannot be both true and false simultaneously. So, if you are unhappy with the idea that (A → B) is true whenever A is false, then perhaps you should consider what would happen if it were false instead. This is what the truth-matrix for implication would look like if we made this change:

??? t f
t t f
f f f

Does this remind you of anything? If you look back at the definitions given above for the logical connectives, you will see that the revised table is identical to that given for conjunction. In other words, the changes mean that implication now has the same meaning, logically speaking, as conjunction. But this cannot be correct, since it implies that, say, if it is raining, then it is snowing means the same as it is raining and it is snowing . Illogical!



OK, I can see that making A -> B false whenever A is false isn't right, but I still don't really understand why it should be true in these cases.

If you aren't convinced yet, then you might consider the following story. Whilst boldly going through the fourth sector some time ago, the Starship Enterprise developed engine trouble in the region of the Karzanian Empire. An envoy of the Karzanian people made contact and stated that:

 

If you beam me up, then I will help you

Now, the Karzanians are a war-like race and generally acknowledged to be the biggest fibbers in the known universe. Kirk and Spock considered the options:

  1. If we beam the Karzanian up and he helps us, then he has certainly spoken the truth and is no liar.
  2. If we do not beam him up, then whether or not he chooses to help is immaterial: either way he will not have lied.
  3. But if we beam him up and he does not help us, then he has clearly falsified his statement and is a liar.

"It is logical to conclude", Spock told Kirk, "that the Karzanian will not help us if we beam him up, as this is the only way in which he can truly be said to have lied."



Can you explain what is meant by "if and only if"?

This is not an expression that you are likely to use in ordinary speech, nor for the most part do you use it in your written language. In fact, it only really seems to crop up in mathematical proofs and logic textbooks aimed at unsuspecting first year students of computing.

We might say that  "if and only if" expresses bi-implication. That's bi-implication, as opposed to simple  implication, because it actually corresponds to two implications. So, to say:

"A if and only if B"

really amounts to saying

"if A then B"
&
"if B then A"

Here is a simple example to illustrate the use of "if and only if":

"Today is Bill's birthday if and only if today is the 17th December"

in other words:

"if today is the 17th December, then today is Bill's birthday"
&
"if today is Bill's birthday, then today is the 17th December"


How do I test for logical equivalence?

We have looked at more than one way of testing logical equivalence in the course.. Suppose that you are given two statements of the propositional calculus A and B. One way of testing logical equivalence involves constructing a truth table, and then checking to see that the statements A and B have the same truth value on each row of the table.

For example, consider the statements $(p \rightarrow q) \wedge \neg q$ and $\neg (p \vee q)$. To test whether these statements are logically equivalent, we construct a truth table as follows:


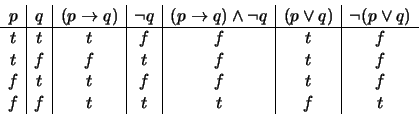
\begin{displaymath} \begin{array}{c\vert c\vert c\vert c\vert c\vert c\vert c} ... ...& t & f & t & t & f \\ f & f & t & t & t & f & t \end{array} \end{displaymath}

Now look at the columns for $(p \rightarrow q) \wedge \neg q$ and $\neg (p \vee q)$. If you compare them row by row, what do you see?

The same truth value appears in each column on the same row. It can be concluded that the two statements are logically equivalent.



OK, I can see that now, but what if I don't want to use truth tables to test logical equivalence?

Another way of testing logical equivalence is to use the so-called 'laws of logical equivalence'. These laws are statements of the form $A \sim B$, meaning ``the statement $A$ is logically equivalent to the statement $B$''. Given a limited set of statements of this kind, it is possible to demonstrate many other logical equivalences.

The laws of logical equivalence were discussed in the fourth lecture of your course. A complete set of laws can be found in most logic textbooks: see e.g. Kelly p.12 or Nissanke pp. 48-51.

Here are a few selected examples:


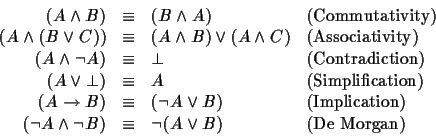
\begin{displaymath} \begin{array}{rcll} (A \wedge B) & \equiv & (B \wedge A) & \... ... B) & \equiv & \neg (A \vee B) & \mbox{(De Morgan)} \end{array}\end{displaymath}

Using just the above laws, I can again show the equivalence of $(p \rightarrow q) \wedge \neg q$ and $\neg (p \vee q)$. The idea is to use the laws to repeatedly re-write one or other of the statements into a logically equivalent expression. If we can transform both statements into the same form, then they are logically equivalant. In the following, I just keep rewriting $(p \rightarrow q) \wedge \neg q$ until I eventually reach the statement $\neg (p \vee q)$.


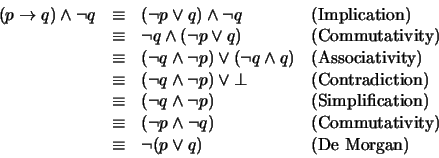
\begin{displaymath} \begin{array}{rcll} (p \rightarrow q) \wedge \neg q & \equiv... ... & \equiv & \neg( p \vee q ) & \mbox{(De Morgan)} \end{array}\end{displaymath}

So again, we have that the two statements are logically equivalent.

 

What is a 'valuation'?

A valuation  is just an assignment of truth values to propositional variables.  In mathematical terms, it's a function mapping from the set of propositional variables to truth value (i.e.  t (true) and f (false))

Erm, sorry, I think I understand roughly what you mean by 'assignment', but what's a 'function'?

OK, a function is just a mapping from from one set of things to another. Here are some examples:

  1. double: the function that maps each integer, say, onto it's double. So, double(3) = 6, double(29) = 58 and so on and so on.
  2. length: the function that maps from words of English, onto their length (measured in terms of the number of letters they contain). So length("bill") = 4, length("antidisestablishmentarianism") = 28, etc;

Note that to qualify as a function, the mapping must assign at most one value to each thing.


Do I need to learn all of the rules for the construction of semantic tableaux?

Yes, you should learn these rules so that you can construct semantic tableaux. The aren't as difficult to remember as you might think and can be related quite easily to the truth tables (so at a push you can work them out from scratch). To refresh your memory you should read your lecture notes or study one of the course texts.


What is this "entailment relation" all about anyway?

Consider the following simple argument:
If the crystals can't stand it, then Scotty gets hysterical.
If Scotty gets hysterical, then Dr. McCoy restrains him.
So, if the crystals can't stand it, Dr. McCoy restrains Scotty.
I think you will agree that the final statement (the conclusion) appears to follow from the previous two statements (the premises). We might say that the conclusion is a logical consequence of the premises: if the premises are true, then the concluding statement must also be true.

Now semantic entailment is really just a formalisation of this notion of logical consequence; it is intended to capture the idea that one statement follows logically from some given set of other statements.



OK, I understand that entailment is meant to capture something about logical consequence but how does it do that, I mean, how do you define it?

The entailment relation is defined in  semantic terms. That is to say, it is defined in terms of the notions true and false. Let us first introduce some notation for writing down statements about entailment.  For G a set of statements and A a statement we will write

"G |= A"

to mean

"G entails A"

Now here is the definition of the entailment relation:

 
G |= A  if and only if whenever every statement  in G is true, the statement A is true.


Now, that's really quite a short definition, though it is perhaps not easy to understand in one go. For one thing, it uses the phrase  "if and only if". You may wish to refresh your memory about if and only if before continuing.

Really, what the definition comes down to is this. By saying "G entails A" all we're really saying is "whenever every statement in G is true, then the statement A is true".

Beam me up to Contents