Seminar IV

The following exercises are concerned with the Propositional Calculus as a formal, deductive system. The following formalization (axioms and inference rules) is assumed:

Axiom Schemas:

S1

$(A \rightarrow (B \rightarrow A))$

S2

$((A \rightarrow (B \rightarrow C)) \rightarrow ((A \rightarrow B) \rightarrow (A \rightarrow C)))$

S3

$(((\neg A) \rightarrow (\neg B)) \rightarrow (B \rightarrow A))$

Inference Rule:

MP

From $A$ and $A \rightarrow B$, infer $B$

I. Decide whether or not the following sentences are axioms (i.e. instances of the axiom schemas given above):

1. $(p \rightarrow (p \rightarrow p))$
2. $(p \rightarrow (q \rightarrow r))$
3. $((p \rightarrow ((\neg q) \rightarrow (\neg r))) \rightarrow ((p \rightarrow (\neg q)) \rightarrow (p \rightarrow (\neg r))))$
4. $(((\neg p) \rightarrow (\neg \neg p)) \rightarrow (p \rightarrow (\neg p)))$

II. Justify the steps in the following proof that $(p \rightarrow p)$ is deducible from $p$ (that is, $\{p\} \vdash (p \rightarrow p)$):

$$\begin{array}{lll} (1) & p & \\ (2) & (p \rightarrow (p \rightarrow p)) & \\ (3) & (p \rightarrow p) \end{array}$$

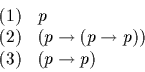
III. Construct proofs of the following:

1. $\vdash (p \rightarrow (p \rightarrow p))$
2. $\{p, (p \rightarrow q)\} \vdash q$
3. $\{q\} \vdash (p \rightarrow q)$