| Discrete Dynamics Lab |
Update
ddlabx11
New options for Automatic Derrida plots for sets of rules,
equivalence classes and rule clusters. |
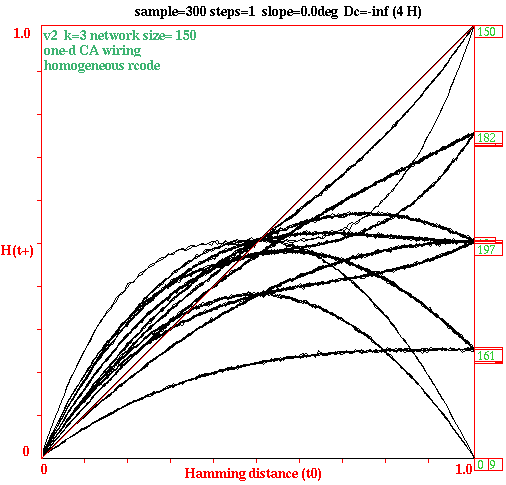
Automatically generated set of Derrida plots for ECA rule-space, n=150. DDLab is able to filter out and list the 88 equivalence or 48 rule-clusters of the 256 ECA rules. Its notable that there are only 14 independent plots. |
DDLab has been updated at regular intervals since its release in 1995.
Its precursor was the Atlas software included on diskette
inside the back cover of "The Global Dynamics of Cellular Automata". For a list and download of this and older versions click here. Below are links to descriptions of previous updates, Jan 2013 June 2012 Nov 2005 Dec 2003 July 2001 Feb 1999 Sept 1997 |
download
ddlabx11 for Linux, Mac, Cygwin and DOS
#: s n r nr D
In EDD#18.1.1, the transform prompt for a single rule is extended to show
the equivalence classes or rule clusters in the terminal.
Enter EquivClass-E for the equivalence class, giving,
Enter EquivClass-R for the rule cluster, giving,>
11539fa3 n=3a063577 r=541724ef nr=08db17d5 ...for example, rcode v2k5,
The method works for rcode, tcode and kcode.
Automatic Derrida plots for sets of rules, equivalence classes and rule clusters.
The main application of the Derrida plot (described in EDD#22) has been as an order-chaos measure for large RBN
networks in the context of models of genetic regulatory networks, where the canalyzing
inputs can be tuned to move the dynamics between order and chaos (EDD#15). However, the
Derrida plot also provides Liapunov-like insights into CA rules; new options allow automatic plots
of sets of rules in ascending decimal order, filtering out equivalent binary rcode and tcode, and
listing equivalence classes and rule clusters.
Its of some interest to compare the Derrida plots of various CA rule spaces, for example the 256
elementary (ECA) rules (v2k3 rcode), or the 64 v2k5 totalistic rules (tcode or kcode).
In the "Global Dynamics of Cellular Automata" (GDCA) it was shown that a rule has equivelent rules
by negative, reflection and negative+reflection transformations, making an equivalence class were
all behavior is strictly equivalent. A further complimentary transformation will group the rules
into a rule cluster. Complimentary rules, though usually not equivalent, share some important
behavior measures, including the Z-parameter and G-density (EDD#24.9), and the in-degree
histogram (EDD#24.6). As set out in GDCA, the 256 elementary rules fall into 88 equivalence
classes and 48 rule clusters. The 64 v2k5 totalistic rules fall into 36 equivalence classes and 20 rule
clusters.
Experiment confirms, as expected, that the Derrida plots for the rules in an equivalence class
will be the same (subject to sampling variation) as if plotting the same rule, and this turns
out also to be true of the complimentary rules -- the rule cluster has the same Derrida properties.
Its possible to automatically generate the Derrida plots for binary (v=2) rule-spaces according to
equivalence classes or rule clusters, or for (v>=2) rules, counting up from the start rule in decimal.
The procedure works for rcode in SEED-mode, and for kcode or tcode in TFO-mode. However,
rule-tables must be within the limits in table 16.1 for expressing the rule as a decimal number.
The prompt in EDD#22.5 "Completing the Derrida Plot" is extended as follows,.
To automatically generate the Derrida plots, enter 1 for equivalence classes, 2
for rule clusters, or 3 for just a sequence of rules. In each case the initial
rule, selected in EED#16 or revised with reset-r in section EDD#22.5 starts of the sequence, counting
up, so to obtain an orderly and complete sequence of rules for an entire rule-space, the initial rule
should be set to decimal rule 0 (zero).
Add k to retain previous plots
for a multiple automatic plot, for example, enter 1k, 2k or 3k. If k
is not added each new automatic plot is displayed separately.
Starting with rule 0 for equivalence classes, just the lowest decimal rule will be plotted (as the
representative rule) and the others skipped and filtered from the remaining list. For rule clusters,
the compliment of the representative rule is also plotted, and its remaining equivalence class is
also skipped and filtered from the remaining list. The rules making up equivalence classes or rule
clusters are displayed in the terminal window (xterm) for Linux-like systems (Left panel), so
this is a useful result in itself -- Derrida parameters can be minimised if this is the only data required.
summary of updates
(EDD#x.x.x refers to the relevant chapter or
section in "Exploring Discrete Dynamics")
Return to the
Discrete Dynamics Lab home page.
48 rule clusters of the 256 v2k3 ECA
there are 88 equivalence classes
Automatic output in the terminal:
1: 0 255 0 255 -inf
255 0 255 0 -inf (-nan)
2: 1 127 1 127 -0.457
254 128 254 128 -0.377 (-0.080)
3: 2 191 16 247 -0.445
253 64 239 8 -0.426 (-0.020)
4: 3 63 17 119 -0.036
252 192 238 136 0.014 (-0.050)
5: 4 223 4 223 -0.428
251 32 251 32 -0.423 (-0.005)
6: 5 95 5 95 -0.014
250 160 250 160 -0.021 (0.007)
7: 6 159 20 215 0.572
249 96 235 40 0.559 (0.013)
8: 7 31 21 87 0.324
248 224 234 168 0.302 (0.023)
9: 9 111 65 125 0.509
246 144 190 130 0.575 (-0.066)
10: 10 175 80 245 -0.034
245 80 175 10 0.007 (-0.041)
11: 11 47 81 117 0.304
244 208 174 138 0.328 (-0.024)
12: 12 207 68 221 -0.023
243 48 187 34 -0.042 (0.018)
13: 13 79 69 93 0.287
242 176 186 162 0.315 (-0.029)
14: 14 143 84 213 0.324
241 112 171 42 0.299 (0.025)
15: 15 15 85 85 -0.000
240 240 170 170 -0.000 (0.000)
16: 18 183 18 183 0.586
237 72 237 72 0.577 (0.008)
17: 19 55 19 55 0.302
236 200 236 200 0.304 (-0.002)
18: 22 151 22 151 1.143
233 104 233 104 1.136 (0.007)
19: 23 23 23 23 0.544
232 232 232 232 0.582 (-0.038)
20: 24 231 66 189 0.588
231 24 189 66 0.582 (0.006)
21: 25 103 67 61 0.800
230 152 188 194 0.785 (0.015)
22: 26 167 82 181 0.784
229 88 173 74 0.807 (-0.023)
23: 27 39 83 53 0.579
228 216 172 202 0.574 (0.006)
24: 28 199 70 157 0.807
227 56 185 98 0.794 (0.013)
25: 29 71 71 29 0.589
226 184 184 226 0.601 (-0.011)
26: 30 135 86 149 1.003
225 120 169 106 0.992 (0.012)
27: 33 123 33 123 0.576
222 132 222 132 0.563 (0.013)
28: 35 59 49 115 0.297
220 196 206 140 0.318 (-0.021)
29: 36 219 36 219 0.552
219 36 219 36 0.564 (-0.011)
30: 37 91 37 91 0.774
218 164 218 164 0.788 (-0.014)
31: 38 155 52 211 0.778
217 100 203 44 0.800 (-0.022)
32: 41 107 97 121 1.150
214 148 158 134 1.124 (0.026)
33: 43 43 113 113 0.577
212 212 142 142 0.560 (0.016)
34: 45 75 101 89 0.983
210 180 154 166 0.982 (0.002)
35: 46 139 116 209 0.583
209 116 139 46 0.574 (0.009)
36: 50 179 50 179 0.306
205 76 205 76 0.333 (-0.027)
37: 51 51 51 51 -0.000
204 204 204 204 -0.000 (0.000)
38: 54 147 54 147 0.988
201 108 201 108 0.968 (0.020)
39: 57 99 99 57 0.981
198 156 156 198 0.971 (0.010)
40: 58 163 114 177 0.578
197 92 141 78 0.566 (0.012)
41: 60 195 102 153 0.980
195 60 153 102 0.986 (-0.006)
42: 62 131 118 145 0.798
193 124 137 110 0.785 (0.013)
43: 73 109 73 109 1.153
182 146 182 146 1.133 (0.021)
44: 77 77 77 77 0.571
178 178 178 178 0.593 (-0.022)
45: 90 165 90 165 0.988
165 90 165 90 0.983 (0.005)
46: 94 133 94 133 0.794
161 122 161 122 0.815 (-0.022)
47: 105 105 105 105 1.555
150 150 150 150 1.555 (0.000)
48: 126 129 126 129 0.569<
129 126 129 126 0.578 (-0.009)
equivalence classes and rule clusters.
110 n=137 r=124 nr=193 ...for example, an ECA rule v2k3,
where 110=start rule n=negative r=reflection nr=negative+reflection
eeac605c n=c5f9ca88 r=abe8db10 nr=f724e82a ...the compiliments (shown in hex)
Last modified: May2013