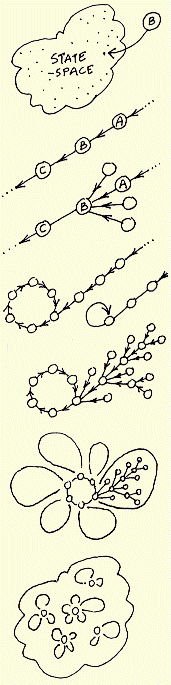
might be 1010...0110.
State-space is made up of all 2n states, the space of all
possible bitstrings or patterns.
Part of a trajectory in state-space, where C is a successor
of B, and A is a predecessor, pre-image, of B,
according to
the dynamics on the network.
The state B may have other pre-images besides A, the total
is the in-degree. The pre-image states may have their own
pre-images or none. States without pre-images are known
as garden-of-Eden states.
Any trajectory must sooner or later encounter a state that
occurred previously - it has entered an attractor cycle. The
trajectory leading to the attractor is a transient. The period
of the attractor is the number of states in its cycle, which may
be just one - a point attractor.
Take a state on the attractor, find its pre-images (excluding
the pre-image on the attractor). Now find the pre-images of
each pre-image, and so on, until all garden-of-Eden states are
reached. The graph of linked states is a transient tree rooted
on the attractor state. Part of the transient tree is a subtree
defined by its root.
Construct each transient tree (if any) from each attractor state.
The complete graph is the basin of attraction. Some basins of
attraction have no transient trees, just the bare ``attractor''.
Now find every attractor cycle in state-space and construct
its basin of attraction. This is the basin of attraction field
containing all 2n states in state-space, but now linked
according to the dynamics on the network. Each discrete
dynamical network imposes a particular basin of attraction
field on state-space.