Research Methods 1: Statistics Problem-Sheet 7: Chi-Square:

Research Methods 1: Statistics Problem-Sheet 5: Chi-Square:

1. A sample of 100 voters are asked which of four candidates they would vote for in an election. The number supporting each candidate is given below:

Higgins Reardon White Charlton

41 19 24 16

Do the data suggest that all candidates are equally popular? [Chi-Square = 14.96, with 3 d.f.: p<0.05].

2. Children of three ages are asked to indicate their preference for three photographs of adults. Do the data suggest that there is a significant relationship between age and photograph preference? What is wrong with this study? [Chi-Square = 29.6, with 4 d.f.: p<0.05].

Photograph:

A B C

Age of child: 5-6 years: 18 22 20

7-8 years: 2 28 40

9-10 years: 20 10 40

3. A study of conformity using the Asch paradigm involved two conditions: one where one confederate supported the true judgement, and another where no confederate gave the correct response

Support: No Support:

Conform: 18 40

Not Conform: 32 10

Is there a significant difference between the "support" and "no support" conditions in the frequency with which individuals are likely to conform? [Chi-Square = 19.87, with 1 d.f.: p<0.05. OR: Chi-Square = 18.1. See the comment at the end of this handout].

4. A researcher is interested in sex differences in social play in cats. She observes sixteen kittens (eight male and eight females), and records the sex of the participants in 500 play-bouts, taking a note of the sex of the animal initiating a bout and the sex of the animal who responds to the initiation. Are there sex-differences in the kittens' play? Perform a Chi-Square test on these data. Is there anything wrong with doing this test? [Chi-Square = 3.97, with 1 d.f.: not significant. OR: Chi-Square = 3.58. See the comment at the end of this handout].

respondent

male female

initiator of bout: male: 200 150

female: 100 50

5. We want to test whether short people differ with respect to their leadership qualities (Genghis Khan, Adolf Hitler and Napoleon were all stature-deprived, and how many midget MP's are there?) The following table shows the frequencies with which 43 short people and 52 tall people were categorised as "leaders", "followers" or as "unclassifiable". Is there a relationship between height and leadership qualities? [Chi-Square = 10.71, with 2 d.f.: p<0.01].

6. The Government decide to find out how many people use various kinds of transport to commute from Brighton to London each day. They go to Victoria train station, and ask a random sample of 80 individuals what type of transport they use. Here are the raw data, coded as follows: "1" if the person uses a car; "2" if they use a train; "3" if they walk; and "4" if they fly. The null hypothesis is that all four forms of transport are used equally frequently by the general commuting public.

(a) Draw a frequency histogram of these data.

(b) Perform a Chi-Square Goodness of Fit test on these data.

1,4,2,3,4,4,3,4,4,2 2,2,1,4,3,3,2,2,2,2

3,2,4,4,3,2,1,1,2,3 4,4,3,3,2,1,3,2,4,3

2,1,2,2,2,1,2,3,2,4 3,2,2,3,4,2,3,4,2,2

2,1,2,1,2,2,2,3,4,3 2,2,1,3,2,2,2,1,2,2

What problems are there with this study?

Chi-Square in the 1 d.f. case, and the use of Yates' Correction:

If you have only 1 d.f., as in the case of a 2x2 contingency table, some textbooks suggest that you apply what's known as "Yates' Correction" to the Chi-Square formula. When the d.f. are very small, (and you can't get much smaller than 1!), the Chi-Square sampling distribution becomes increasingly distorted. As a consequence, the obtained value of Chi-Square tends to overestimate the "true" discrepancy between the observed and expected frequencies. Yates' correction is a simple bodge that makes the formula produce a lower value of Chi-Square than it otherwise would do. This makes the Chi-Square test more "conservative": i.e., it makes it harder to get a statistically significant result. Here is the "corrected" formula:

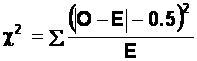
In English, this means you do the following:

(a) Get the absolute value (i.e., ignore the sign) of each observed frequency minus its accompanying expected frequency. (The vertical lines mean "ignore the sign of").

(b) From each of these absolute values, subtract 0.5.

(d) Add together all of the results of step (c).

(e) Finally, look up the value of Chi-Square in the usual way.

Statisticians are divided about the need for Yates' correction: some say you should use it, others say it doesn't matter, and some say it makes things worse! Consequently, the answers to the problems on this sheet have been calculated both ways. The normal-type answers are what you would get if you did not use Yates' correction, and the italic-type answers are what you would get if you did. Either is acceptable, as long as you make it clear whether or not you used Yates' correction. Remember - if you do use it, it is only to be used when you have just one degree of freedom.

First-year Research Methods: Worked Solutions to Problem Sheet 5:

Question 1:

A Chi-Squared Goodness-of-Fit test is appropriate here. The null hypothesis is that there is no preference for any of the candidates: if this is so, we would expect roughly equal numbers of voters to support each candidate. Our expected frequencies are therefore 100/4 = 25 per candidate.

O	41	19	24	16
E	25	25	25	25
(O-E)	16	-6	-1	-9
(O-E)²	256	36	1	81
(O-E)² --------- E	10.24	1.44	0.04	3.24

Adding together the last row gives us our value of c² :

(O - E)²

å ----------------- = 10.24+ 1.44 + 0.04 + 3.24 = 14.96, with 4 - 1 = 3 degrees of freedom.

The critical value of Chi-Square for a 0.05 significance level and 3 d.f. is 7.82. Our obtained Chi-Square value is bigger than this, and so we conclude that our obtained value is unlikely to have occurred merely by chance. In fact, our obtained value is bigger than the critical Chi-Square value for the 0.01 significance level (13.28). In other words, it is possible that our obtained Chi-Square value is due merely to chance, but highly unlikely: a Chi-Square value as large as ours will occur by chance only about once in a hundred trials. It seems more reasonable to conclude that our results are not de to chance, and that the data do indeed suggest that voters do not prefer the four candidates equally.

Question 2:

		photograph:
age of child:	A:		B:	C:	row totals:
5-6 years	18		22	20	60
7-8 years	2		28	40	70
9-10 years	20		10	40	70
column totals:	40		60	100	200

(a) Work out the row, column and grand totals (as shown in the shaded parts of the table, above).

(b) Work out the expected frequencies, using the formula:

(row total * column total)

E = --------------------------------------

grand total

For each cell of the above table, this gives us:

O:	18	22	20	2	28	40	20	10	40
E:	12	18	30	14	21	35	14	21	35

Next, work out (O - E):

(O-E):

-10

-12

Square each of these, to get (O - E)²:

(O - E)²:

100

144

121

Divide each of the above numbers by E, to get (O - E)² / E:

(O - E)²

----------

0.89

3.33

10.29

2.33

0.71

2.57

5.76

0.71

Chi-squared is the sum of these:

c² = 29.60.

d.f. = (rows - 1) * (columns - 1) = 2 * 2 = 4.

The critical value of Chi-Square in the table for a 0.001 significance level and 4 d.f. is 18.46. Our obtained Chi-Square value is bigger than this: therefore we have a Chi-Square value which is so large that it would occur by chance only about once in a thousand times. It seems more reasonable to accept the alternative hypothesis, that there is a significant relationship between age of child and photograph preference.

Question 3:

Here we have a 2x2 contingency table. Chi-Square is the appropriate test to use, but since we have 1 d.f., we will modify the formula to include "Yates' correction for continuity".

	support	no support	row totals:
conform:	18	40	58
not conform:	32	10	42
column totals:	50	50	100

(a) Calculate the row, column and grand totals.

(b) Calculate the expected frequency for each cell of the table, by multiplying together the appropriate row and column totals and then dividing by the grand total.

(c) Subtract each expected frequency from its associated observed frequency; but then apply Yates' correction, by subtracting 0.5 from the absolute value of each O-E value. (The vertical bars in the formula mean "ignore any minus signs").

O:	18	40	32	10
E:	29	29	21	21

Next, work out (O - E):

(|O-E|- 0.5):

10.5

Square each of these, to get (O - E)²:

(|O-E|- 0.5)²:

110.25

Divide each of the above numbers by E, to get (O - E)² / E:

(O - E)²

-----------

3.80

5.25

Chi-squared is the sum of these:

c² = 18.10.

d.f. = (rows - 1) * (columns - 1) = 1 * 1 = 1.

Our obtained value of Chi-Squared is bigger than the critical value of Chi-Squared for a 0.001 significance level. In other words, there is less than a one in a thousand chance of obtaining a Chi-Square value as big as our obtained one, merely by chance. Therefore we can conclude that there is a significant difference between the "support" and "no support" conditions, in terms of the frequency with which individuals conformed.

Question 4:

		respondent:
initiator:	male		female	row totals:
male	200		150	350
female	100		50	150
column totals:	300		200	500

(a) Calculate the marginal totals and expected frequencies.

The expected frequencies are obtained by multiplying the row total by the column total, and then dividing by the grand total. For example, the expected frequency for male-male play is (350*300)/500 = 210; the expected frequency for male-female play is (150*200)/500 = 60; and so on. Expected frequencies are shown in brackets below:

		respondent:
initiator:	male		female	row totals:
male	200 (210)		150 (140)	350
female	100 (90)		50 (60)	150
column totals:	300		200	500

NB: the expected frequencies should add up to the same Grand Total (500 in this case) as the observed frequencies!

(b) Since we have a 2x2 table (and hence 1 d.f.) we will work out Chi-Square incorporating Yates' correction for continuity. For each cell in the table, work out:

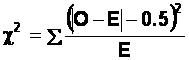
This gives us the following numbers:

		respondent:
initiator:	male		female
male	0.4298		0.6446
female	1.0028		1.5042

(c) Adding these together gives us our value of Chi-Square: 3.581, with 1 d.f. This is smaller than the critical value of Chi-Square for 1 d.f. at the 0,.05 significance level, which is 3.841. We would therefore conclude that the frequencies with which male and female animals play together in opposite-sex and liked-sexed pairs do not differ from those that we would expect by chance.

In practice, there is a problem with this analysis which invalidates the Chi-Square test: we have 500 observations from only 16 animals, which means that each animal must have contributed more than observation to the total. This means that the observations are not independent - thus violating an important assumption for the use of the Chi-Square test.

Question 5:

Expected frequencies are in brackets:

		height:
	short		tall	row totals:
leader:	12 (19.92)		32 (24.08)	44
follower:	22 (16.29)		14 (19.71)	36
unclassifiable:	9 (6.79)		6 (8.21)	15
column totals:	43		52	95

Chi-Square = 3.146 + 2.602 + 1.998 + 1.652 + 0.720 + 0.595 = 10.712, with 2 d.f.

10.712 is bigger than the tabulated value of Chi-Square at the 0.01 significance level. We would conclude that there seems to be a relationship between height and leadership qualities. Note that we can only say that there is a relationship between our two variables, not that once causes the other. There could be all kinds of explanations for such a relationship.

Question 6:

Our 80 subjects fall into four transport categories as follows:

type of transport:
car (1)	train (2)	walk (3)	fly (4)
11	36	18	15

Our null hypothesis is that each form of transport is used equally frequently. Therefore our expected frequencies are (80/4) = 20, 20, 20 and 20. The appropriate analysis is a Chi-Squared Goodness-of-Fit test.

Take each observed frequency; subtract 20; square the result; and then divide by 20. This gives 4.05, 12.80, 0.20 and 1.25. Adding these values together gives us our value of Chi-Square: 18.30, with 3 d.f., p<0.001. In other words, our obtained frequencies are markedly different from those that we would expect to obtain by chance. Strictly speaking, this is all we can say. However, "eyeballing" the data suggests that more people travel by train than we would expect, and fewer by car (well, these are fictional data!)

The problem with this study lies not in the statistical analysis, but in the way that the data were obtained: standing in a train station is likely to bias the sample in favour of people travelling by train.